Quando aprendemos listas, nossos exemplos todos tratavam de listas com valores escalares. Dizemos que uma variável é de um tipo escalar porque os valores possíveis são simples e indivisíveis, como um número inteiro ou um número de ponto flutuante. Muitas vezes, também vamos olhar para strings como uma unidade (sem se preocupar com quais partes a formam), então também chamaremos as strings de valores escalares.

Restringir-nos a listas de valores escalares pode simplificar nossos algoritmos, mas também limita o tipo de estrutura que conseguimos representar. Para muitas aplicações, elas são tudo do que precisamos.

Escreva um programa que leia as notas de 10 exercícios de um estudante e calcule a média dos 9 exercícios com maiores notas.

Esse problema é mais simples do que muitos outros que já fizemos, mas vamos resolvê-lo agora com uma atenção especial à representação dos dados. Queremos representar as notas de um aluno, então vamos armazená-las em um lista de notas.

Em Python, os tipos das variáveis não estão anotadas juntamente com os nomes das variáveis. Por isso, precisamos tomar bastante cuidado em como nomeamos nossas variáveis, para ficar claro quando estamos lidando com um valor escalar, ou com uma lista de escalares. Para isso, devemos utilizar os nomes consistentemente:

• Uma nota é um escalar do tipo float. Vamos denotar variáveis de tipos escalares sempre pelo nome nota.
• Uma lista de notas é do tipo list e cada elemento dessa lista é um escalar que representa uma nota. Vamos denotar variáveis de tipo lista de escalares sempre pelo nome lista_notas.

Uma vez que já sabemos como representar os dados na memória do computador, já podemos passar a escrita do algoritmo. Você deve escrever um algoritmo e construir o seu programa incrementalmente. Eu vou adiantar tudo isso e mostrar o programa já pronto.

NUMERO_EXERCICIOS = 3

def ler_lista_notas(n):
    """Devolve uma lista de n notas lidas do teclado"""
    lista_notas = []
    for _ in range(n):
        print("Digite a próxima nota: ")
        nota = float(input())
        lista_notas.append(nota)
    return lista_notas

def calcular_media_excluida(lista_notas, indice_excluida):
    """Devolve a média de lista_notas excluindo-se
    a nota de índice indice_excluida"""
    soma = 0.0
    for i, nota in enumerate(lista_notas):
        if i != indice_excluida:
            soma = soma + nota
    media = soma / (len(lista_notas) - 1)
    return media

def obter_indice_menor(lista_notas):
    """Devolve o índice da menor nota"""
    indice_menor = 0
    menor_nota = lista_notas[0]
    for i, nota in enumerate(lista_notas):
        if nota < menor_nota:
            menor_nota = nota
            indice_menor = i
    return indice_menor

def main():
    print("Digite as notas dos exercícios:")
    lista_notas = ler_lista_notas(NUMERO_EXERCICIOS)
    indice_menor = obter_indice_menor(lista_notas)
    media = calcular_media_excluida(lista_notas, indice_menor)
    print(f"A média excluindo a pior nota é {media}")

main()

Leia esse programa com atenção. Estude o que cada função faz. Não continue lendo este texto até que tenha entendido e internalizado esse programa.

É claro que uma professora não gostaria de usar esse programa, porque ela não tem apenas um estudante. É bem possível que sua turma tenha 100 estudantes. Então ela teria que executar esse programa 100 vezes e tomar nota manualmente da média de cada um. Pior, pode ser que a professora decida que irá excluir a nota do mesmo exercício para a turma inteira, então esse programa já não seria mais útil. Vejamos por quê:

1. para descobrir a média da turma, fixamos um exercício, e percorremos a lista de notas de todos os estudantes para esse exercício

2. para calcular a média de um estudante, fixamos esse estudante e percorremos a lista de notas de todos os exercícios para esse estudante

Agora deve estar claro porque nos restringir a listas de escalares é insuficiente: precisamos tanto da lista de notas de todos os exercícios para um estudante, quanto da lista de notas de um exercício para todos estudantes. Para deixar esse problema mais concreto, vamos resolver o seguinte problema:

Escreva um programa que leia a notas de 10 exercícios de 100 estudantes e depois:

1. calcule a média da turma para cada exercício;
2. descubra o exercício com menor média da turma;
3. calcule a média de cada estudante, excluindo-se esse exercício.

Antes de começar a escrever nosso algoritmo e nosso programa, precisamos pensar na maneira como vamos representar os dados na memória. O que muda é que agora, além de representar as notas dos exercícios de um estudantes, precisamos guardar a tabela de notas da turma inteira. Vamos estender a nossa convenção:

• Uma nota é um escalar. Vamos denotar variáveis de tipos escalares sempre pelo nome nota.
• Um estudante tem um lista de notas. Vamos denotar variáveis de tipo lista de escalares sempre pelo nome lista_notas;
• A tabela de notas da turma é uma lista de lista de notas. Vamos denotar variáveis de tipo lista de lista de escalares pelo nome tabela_notas.

De novo, escrevemos um algoritmo e implementamos esse programa incrementalmente. Vamos omitir esse processo e ver o resultado.

NUMERO_EXERCICIOS = 10
NUMERO_ESTUDANTES = 100

def ler_lista_notas(n):
    """Devolve uma lista de n notas lidas do teclado"""
    lista_notas = []
    for _ in range(n):
        print("Digite a próxima nota: ")
        nota = float(input())
        lista_notas.append(nota)
    return lista_notas

def ler_tabela_notas(m, n):
    """Devolve a tabela de notas de m estudantes
    com n notas de exercícios cada, lidas do teclado"""
    tabela_notas = []
    for _ in range(m):
        print("Digite as notas dos exercicios do proximo estudante: ")
        lista_notas = ler_lista_notas(n)
        tabela_notas.append(lista_notas)
    return tabela_notas

def calcular_lista_medias(tabela_notas):
    """Devolve uma lista com as médias dos exercício"""
    m = len(tabela_notas)  # número de estudantes
    n = len(tabela_notas[0])  # número de exercícios

    lista_medias = []
    for j in range(n):
        soma = 0
        for i in range(m):
            soma = soma + tabela_notas[i][j]
        media = soma / m
        lista_medias.append(media)

    return lista_medias

def obter_indice_menor(lista_notas):
    """Devolve o índice da menor nota"""
    indice_menor = 0
    menor_nota = lista_notas[0]
    for i, nota in enumerate(lista_notas):
        if nota < menor_nota:
            menor_nota = nota
            indice_menor = i
    return indice_menor

def calcular_media_excluida(lista_notas, indice_excluida):
    """Devolve a média de lista_notas excluindo-se
    a nota de índice indice_excluida"""
    soma = 0.0
    for i, nota in enumerate(lista_notas):
        if i != indice_excluida:
            soma = soma + nota
    media = soma / (len(lista_notas) - 1)
    return media

def main():
    tabela_notas = ler_tabela_notas(NUMERO_ESTUDANTES, NUMERO_EXERCICIOS)
    lista_medias = calcular_lista_medias(tabela_notas)
    indice_menor = obter_indice_menor(lista_medias)
    for i in range(NUMERO_ESTUDANTES):
        media = calcular_media_excluida(tabela_notas[i], indice_menor)
        print(f"O estudante {i} tem média {media}")

main()

Mantivemos as três funções do programa anterior. Ser organizado e usar nomes de funções e variáveis consistentes realmente salva a vida! Vamos estudar então as demais funções, a começar pela ler_tabela_notas.

Repare que função ler_tabela_notas é surpreendente parecida com a função ler_lista_notas. Isso não acontece por um acaso. O que ler_lista_notas faz é construir e devolver uma lista de elementos, cada um do tipo float. Do mesmo modo, ler_tabela_notas constrói e devolve uma lista de elementos, mas dessa vez, cada elemento da lista é uma outra lista.

Agora investiguemos calcular_lista_medias. Essa função tem dois laços aninhados. O for externo pode ser lido como para cada exercício j, calcule a média da turma para esse exercício. Então vamos nos concentrar em como calcular a média de um exercício. Já vimos como calcular a média de uma lista de floats antes; aqui, queremos fazer algo parecido. A diferença é que as notas de um exercício em particular estão espalhadas nas várias listas dos alunos. Assim, primeiro precisamos acessar a lista de notas de um aluno, por isso escrevemos tabela_notas[i]. Depois, nesta lista, precisamos acessar a nota do exercício j, então escrevemos tabela_notas[i][j]. Respire um pouco e releia essa função. Agora deve fazer sentido.

Por último, vamos olhar para a função main. As instruções dela já devem ser autoexplicativas (repararam que ela não tem comentários?). Vamos olhar apenas para a chamada à função calcular_media_excluida. Essa função recebe como primeiro parâmetro uma lista de notas. De fato, é exatamente isso que passamos a ela: tabela_notas[i] é a lista de notas do estudante de índice i. Se você se sentir mais confortável, poderia substituir essa linha pelas linhas abaixo. É completamente equivalente!

        lista_notas = tabela_notas[i]
        media = calcular_media_excluida(lista_notas, indice_menor)

Agora que já entendeu o programa acima, execute-o e teste-o. Eu se fosse você modificaria os valores de NUMERO_EXERCICIOS e NUMERO_ESTUDANTES e criaria alguns arquivos de teste. Reflita sobre testes automatizados.

Matrizes

A principal estrutura de dados que criamos no exemplo anterior foi uma lista de lista de escalares! Se quisermos, podemos escrever a nossa tabela de notas como uma tabela de fato. A variável a seguir representa três alunos, cada aluno tem quatro notas.

>>> tabela_notas = [
...   [4.5, 7.6, 8.5, 4.5],
...   [9.9, 8.0, 8.0, 6.0],
...   [0.0, 3.3, 7.0, 8.0],
... ]

Certa uniformidade é relevante. Repare que tabela_notas é uma lista com três listas, cada uma delas com quatro números do tipo float. Uma tabela como essa é normalmente chamada de matriz na Matemática. Em Python, representamos matrizes usando lista de listas. Na verdade, Python não sabe nada sobre matrizes, então poderíamos escrever algo como

>>> destabela_notas = [
>>>   [4.5, 4.5],
>>>   [9.9, 8.0, 8.0, 6.0],
>>>   ["zero", 3],
>>> ]

que o interpretador iria executar, indiferente ao sofrimento dos obsessivos-compulsivos. Então devemos definir matriz de um jeito um pouco mais preciso. Uma matriz é uma lista de listas tal que:

1. todas as listas internas têm o mesmo número de elementos;
2. todos os elementos têm o mesmo tipo escalar.

Algumas vezes, também chamamos listas de arranjos, do inglês arrays (ou vetores, a depender da linguagem). Assim, podemos dizer que uma matriz é um arranjo bidimensional. Também podemos definir arranjos multidimensionais, embora eles sejam menos comuns. Se temos dois estudantes, cada estudante fez três provas e cada prova tem duas questões, então podemos representar as notas das questões como:

>>> notas_questoes = [
...   [[4.0, 5.0],  [3.5, 5.0],  [4.5, 4.0]],
...   [[3.0, 2.0],  [2.5, 0.0],  [0.0, 0.0]],
... ]

Uma variável só é útil quando acessamos o seu valor. Para isso, basta acessar uma lista de cada vez:

>>> # nota do segundo exercício do primeiro estudante
>>> tabela_notas[0][1]
7.6
>>> # nota da primeira questão da segunda prova do segundo estudante
>>> notas_questoes[1][1][0]
2.5

Operações em matrizes

Na Álgebra Linear é comum realizar operações com matrizes, como soma, produto por escalar, produto de matrizes, etc. Como Python não entende o conceito de matriz, tampouco entende como realizar essas operações. Por isso, temos de implementar cada uma delas. Vamos implementar a operação de soma e fazer uma função para testá-la.

def somar_matrizes(a, b):
    """Devolve a soma das matrizes a e b"""
    assert len(a) == len(b), "Números de linhas devem ser iguais"
    assert len(a[0]) == len(b[0]), "Números de colunas devem ser iguais"

    m = len(a)
    n = len(a[0])

    soma = []
    for i in range(m):
        linha = []
        soma.append(linha)
        for j in range(n):
            celula = a[i][j] + b[i][j]
            linha.append(celula)
    return soma

def main():
    a = [
      [5.3, 4.0, 7.5],
      [9.0, 0.0, 9.5],
      [7.0, 6.9, 7.8]
    ]
    b = [
      [1.0, 1.0, 1.0],
      [1.0, 1.0, 1.0],
      [1.0, 1.0, 1.0]
    ]
    soma = somar_matrizes(a, b)
    print(soma)

main()

Na função somar_matrizes decidimos criar a matriz soma linha por linha. Repare que adicionamos linha à matriz soma antes mesmo de adicionar as células que irão compor essa linha. Poderíamos adicionar a linha somente depois, é indiferente.

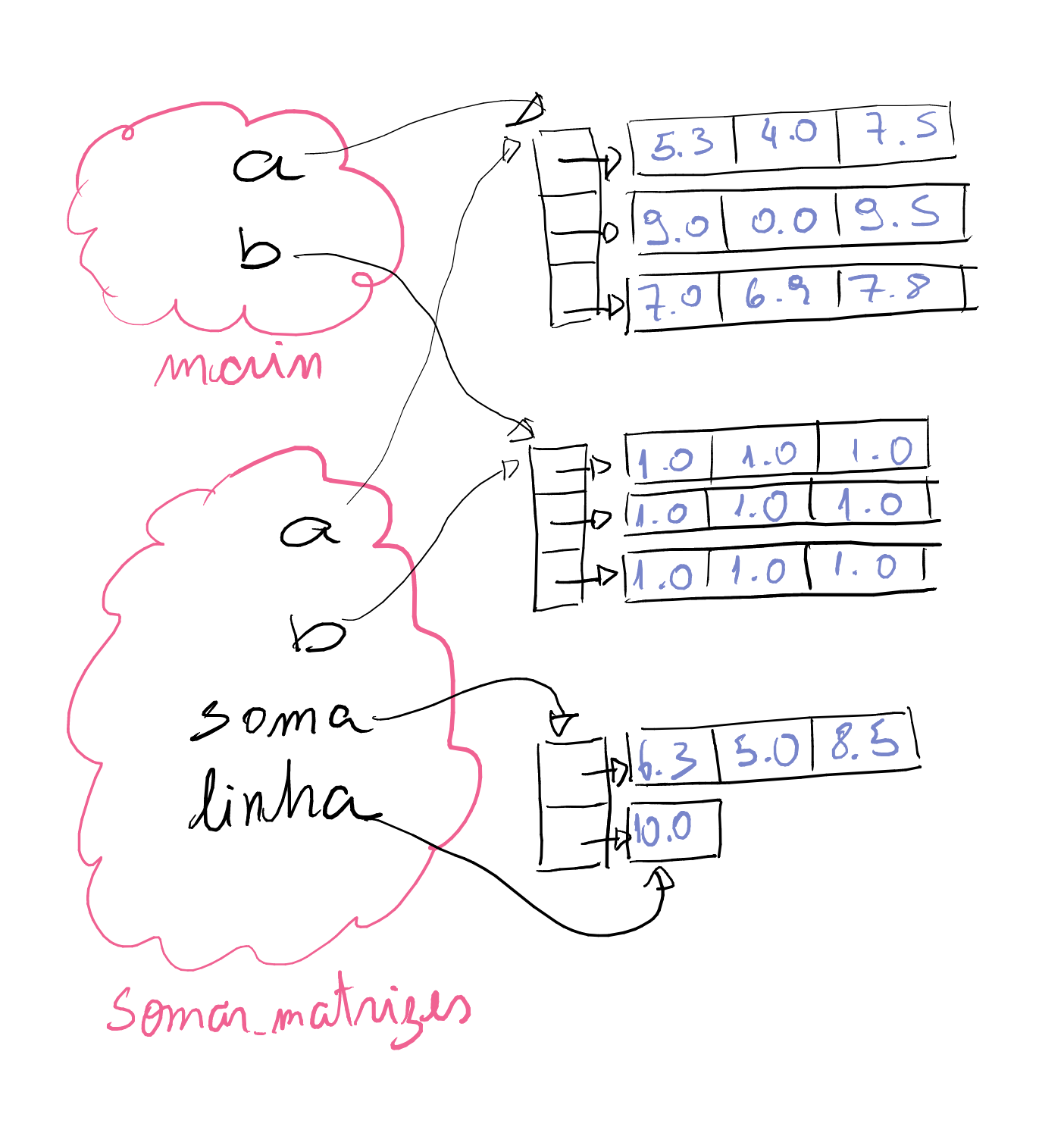
Para entender essa função, é útil simular e olhar para a representação em memória. A figura a seguir mostra a memória do programa ao executar a função somar_matrizes durante a iteração i = 1 do laço externo e ao final da iteração j = 0 do laço interno.

Agora vamos começar a implementar o produto de matrizes. Para isso, vamos relembrar. O produto de uma matriz $A$ de dimensões $m \times l$ por uma matriz $B$ de dimensões $l \times n$ é a matriz $C$ de dimensões $m \times n$, denotada como

$$ C = A \times B $$

em que um elemento $c_{ij}$ é definido pelo produto interno

$$ c_{ij} = \text{(linha $i$ de $A$)} \cdot \text{(coluna $j$ de $B$)}. $$

Dessa vez, vamos primeiro criar uma matriz com zeros $C$ de dimensões $m \times n$ e depois preenchê-la com os valores corretos.

def multiplicar_matrizes(A, B):
    assert len(A[0]) == len(B), "Matrizes devem ser compatíveis"
    m = len(A)
    l = len(B)
    n = len(B[0])
    C = [[0 for _ in range(n)] for _ in range(m)]
    for i in range(m):
        for j in range(n):
            C[i][j] = calcular_produto_interno(A, B, i, j)
    return C

Leia com atenção, faça um desenho da memória e complete a função implementando calcular_produto_interno.

Representação de matrizes

Você deve ter percebido que alguns nomes de variáveis são recorrentes. Isso é intencional para manter a consistência com a notação normalmente utilizada em Álgebra Linear. Assim,

• as matrizes têm dimensão $m \times n$, ou seja, $m$ linhas e $n$ colunas;
• os índices das linhas são normalmente denotados pela letra $i$;
• os índices das colunas são normalmente denotados pela letra $j$.

Enquanto essa convenção é puramente cosmética, utilizar sempre essa notação pode evitar confusões que levam a um grande perda de tempo.

Há uma outra convenção que adotamos quando decidimos representar matrizes: representamos uma matriz como uma lista de linhas. Dessa vez, essa convenção não é meramente cosmética e tem consequências para a forma com que você acessa os elementos de uma matriz e para a maneira com que seu algoritmo manipula a matriz. Não impede que você represente uma matriz como uma lista de colunas, mas só faça isso se tiver uma justificativa.

Uma última palavrinha sobre matrizes em Python: elas não foram feitas pensando em manipular grandes volumes de dados numéricos, nem para realizar operações algébricas facilmente. Por esse motivo, quando precisamos de fato manipular e realizar operações sobre matrizes, normalmente utilizamos uma biblioteca. A mais popular para essa finalidade é a NumPy. Nesta disciplina não iremos utilizá-la, já que para isso seria necessário entender bem programação orientada a objetos (o que não faremos!). Por isso, a não ser que você precise, deixe para estudar essa e outras bibliotecas mais tarde.

Arquivos

Agora que já sabemos trabalhar com coleções de dados um pouco mais complexas do que listas de números ou listas de strings, deve ficar mais latente a necessidade de armazenar dados de maneira permanente. A estratégia de sempre digitar os dados pelo teclado não funciona. Assim, queremos distinguir a memória do computador em

1. Memória volátil. É a memória RAM, utilizada para armazenar variáveis durante a execução do programa. Como regra geral, devemos carregar na memória (i.e., criar variáveis) apenas os dados necessários para realizar a computação. Quando o programa termina, o sistema operacional libera a memória utilizada para outros programas, os dados que não forem armazenados serão perdidos.

2. Memória persistente. É a memória dos discos rígidos, cartões de memória e outros tipos de periféricos que mantém os dados mesmo após o desligamento do computador. Queremos guardar os dados que poderão ser lidos mesmo depois que o programa termina.

Enquanto organizamos a memória RAM utilizando variáveis, a abstração utilizada para organizar a memória persistente são os arquivos. Um arquivo é uma sequência de bytes, armazenados em um dispositivo de memória persistente (disco rígido, CD, fita de dados, USB-Drive etc.) e acessados por meio de um nome.

Os arquivos são identificados por um nome, assim, cada nome deve corresponder a um único arquivo. Normalmente, o nome contém um sufixo, chamado de extensão que correspondente ao tipo dos dados armazenados no arquivo.

Exemplo	Tipo
arq.txt	texto simples
arq.svg	imagem vetorial
arq.c	código-fonte em C
arq.py	código-fonte em Python
arq.html	página da Internet
arq.exe	executável

Enquanto a extensão pode ser utilizada pelo sistema operacional para classificar os arquivos, é importante saber que nada impede que arquivos tenham conteúdo que não correspondem à extensão. Assim, um arquivo arq.txt pode ser o nome de um programa executável e assim por diante.

Os arquivos são organizados no sistema de arquivo por meio de diretórios. Um diretório é um arquivo especial que contém uma lista de arquivos. Esses arquivos podem ser arquivos comuns ou outros diretórios. Assim, os diretórios formam uma hierarquia.

Todo programa executa a partir de algum diretório. Esse é o chamado diretório de trabalho. Para saber qual é o diretório de trabalho em um terminal, digit pwd (ou cd no Windows). Assim, para referenciar outro arquivo, utilizamos o nome simples ou o nome completo na hierarquia de diretórios, dependendo do diretório atual.

• Usamos barra / para separar diretórios (ou contrabarra \ no Windows)

• Usamos uma única barra / para representar a raiz da hierarquia

Vejamos alguns exemplos de caminhos.

• Absolutos, a partir do diretório raiz:

  /home/maria/imagem.jpg
  /home/pedro/arquivo.txt
  /home/pedro/mc102/lab.c
  

• Relativo, a partir do diretório corrente (por exemplo, /home/pedro):

  ../maria/imagem.jpg
  arquivo.txt
  mc102/lab.py
  

Além da sequência de bytes, existem alguns dados associados a um arquivo, que são chamados de atributos de arquivos, entre os quais o proprietário do arquivo, as datas de criação, alteração e acesso, o tamanho em bytes, permissões de acesso etc.

Arquivos de texto e arquivos binários

Os arquivos podem ser classificados em dois grupos:

1. Arquivos de texto
2. Arquivos binários

Um arquivo de texto é uma sequência de caracteres. Como no caso das strings, cada caractere é representado por um ou mais bytes de acordo com alguma tabela de codificação. A codificação mais comum nas aplicações modernas é a chamada UTF-8. Essa codificação representa a tabela de caracteres Unicode, que contém caracteres de quase todas as línguas, além de outros caracteres de controle e, claro, emojis!

Você deveria salvar todos os seus arquivos de texto na codificação UTF-8, mas pode ser que você precise lidar com outras codificações. O importante é entender que arquivos de texto são representados em alguma codificação e, se precisar ler um arquivo armazenado em uma codificação diferente de sua aplicação, será necessário antes converter esse arquivo.

Nem sempre é possível fazer essa conversão sem perda de informação, sobretudo quando usamos aplicações legadas. Por exemplo, pode ser que seu ambiente só reconheça a codificação ASCII, que não possui acentos ou outros caracteres modificados. Pode ser que você tenha um conjunto de arquivos de texto antigos e precise ler esses arquivos por um programa em Python. Quase sempre é preciso se preocupar com a codificação, ou dito de outra forma, quando ignoramos a codificação, quase sempre as coisas vão dar errado.

Um arquivo binário é uma sequência qualquer de bytes. Lembre-se de que um byte é uma sequência de 8 bits. Não podemos armazenar menos de byte em um arquivo. Se você é atento, deverá ter percebido que um arquivo de texto também é um arquivo binário! Na verdade, todos os arquivos são binários, mas normalmente só chamamos de binários aqueles cujos bytes não podem ser interpretados como um arquivo de texto. Isso não significa que os bits e bytes não estejam organizados; significa apenas que a organização do arquivo depende do formato.

Normalmente, mas nem sempre, os primeiros bytes dos arquivos são suficientes para identificar qual é o formato do arquivo. Por exemplo, o comando file de sistemas Unix tenta adivinhar o tipo dos dados de um arquivo, mesmo que a extensão tenha sido modificada.

user@notebook:~/unidades$ file 08-matrizes.html
08-matrizes.html: HTML document, UTF-8 Unicode text, with very long lines
user@notebook:~/unidades$ file virus.jpg
virus.jpg: ELF 64-bit LSB shared object, x86-64, version 1 (SYSV)

Manipulando arquivos

Instruções: Para essa unidade, você deve ler a seção 7 sobre entrada e saída e arquivos do tutorial Python.

Vamos resolver o seguinte exercício:

Escreva um programa que leia um arquivo chamado "palavras.txt" e escreva as palavras que terminam com "s" em um arquivo chamado "plurais.txt" e as demais em um arquivo chamado "singulares.txt".

Abrindo e fechando arquivos

Para acessar um arquivo, precisamos abrir esse arquivo usando uma chamada open(nome_arquivo). Abrir um arquivo é um processo que envolve diversas etapas. Por exemplo, o sistema operacional deve verificar se o arquivo com o nome dado de fato existe e se o usuário tem permissão de acesso a esse arquivo em particular, etc. Quando o arquivo é aberto com sucesso, a função open devolve uma variável com metadados do arquivo. Em particular, essa variável contém um número descritor do sistema operacional para o seu arquivo aberto.

>>> arquivo = open("palavras.txt")
>>> arquivo
<_io.TextIOWrapper name='palavras.txt' mode='r' encoding='UTF-8'>
>>> arquivo.fileno()
3

Uma vez terminado o acesso a um arquivo, é necessário fechá-lo. Fechar um arquivo é muito importante, pois é nesse momento que salvamos as eventuais alterações no disco (a tradução de save como salvar é bastante infeliz, o que queremos fazer é guardar as alterações no disco). Além disso, fechar um arquivo também pede ao sistema operacional para liberar esse arquivo. Dependendo do sistema e do modo como o arquivo foi aberto, outros programas ficaram impedidos de manipular o arquivo enquanto ele não for fechado. Por isso, sempre depois de trabalhar com um aquivo, chamamos a função close

arquivo = open("palavras.txt")
# ...
# acessamos os dados do arquivo
# ...
arquivo.close()

Liberar um recurso depois de usado é tão importante que existe uma sintaxe especial em Python para isso: o bloco with. Assim, ao invés de usar open e close como acima, sempre iremos escrever algo como

with open("palavras.txt") as arquivo:
    # ...
    # acessamos os dados do arquivo
    # ...

Repare que o valor devolvido por open é associado a arquivo e que não precisamos fechar o arquivo explicitamente.

Lendo os dados do arquivo

Quando abrimos um arquivo em um editor de texto, vemos um cursor piscando. Esse cursor indica a posição de leitura e escrita atual do arquivo. Do mesmo modo, quando abrimos um arquivo, o sistema operacional cria um cursor de arquivo, que indica qual é a posição atual do arquivo sendo acessado. O cursor é utilizado para informar a posição no arquivo em estão os próximos bytes a serem lidos, ou a posição no arquivo em que serão escritos os próximos bytes.

O acesso aos dados do arquivo pode se dar de dois modos:

1. Sequencialmente, na ordem em que os dados foram armazenados.
2. Diretamente, obtendo diretamente o dado desejado a partir de sua posição.

Quando lemos um arquivo sequencialmente, lemos cada byte do arquivo, do primeiro ao último, assim como lemos um livro de literatura. No acesso sequencial, o cursor de arquivo nunca retrocede. Quando acessamos um arquivo diretamente, primeiros descobrimos em qual posição está o dado requerido, assim como consultamos o índice de uma lista telefônica. No acesso direto, posicionamos o cursor de arquivo na posição do dado desejado. A cada operação de leitura ou escrita no arquivo, o cursor move-se automaticamente para a próxima posição.

A maneira mais comum de ler um arquivo de dados é interpretar o arquivo como um sequência de linhas e elr . Por esse motivo, Python permite percorrer as linhas de um arquivo como se ele fosse uma lista de strings.

Vamos criar um arquivo de texto com os dados de uma estudante. Não é porque o arquivo é de texto que ele não tem uma estrutura bem definida. No arquivo seguinte, adotamos a seguinte convenção:

1. a primeira linha contém o número de RA;
2. a segunda linha contém o nome completo;
3. a terceira linha contém a data de nascimento;
4. a quarta linha contém o nome da mãe.

123456
 Ana Viva Mariana
29/2/2000
Maria Viva

Para ler esses dados, podemos fazer o seguinte

>>> with open("dados.txt") as arquivo:
...     ra = arquivo.readline()
...     nome_completo = arquivo.readline()
...     nascimento = arquivo.readline()
...     nome_mae = arquivo.readline()
...
>>> ra
' 123456\n'
>>> nome_completo
' Ana Viva Mariana\n'
>>> nascimento
'29/2/2000  \n'
>>> nome_mae
'Maria Viva'

Cada uma das variáveis lidas corresponde a uma linha e é do tipo str. Repare que todas as variáveis lidas terminam com um caractere de nova linha \n, com exceção da última. Isso ocorreu porque quando criei esse arquivo não adicionei um caractere \n na no fim do arquivo, i.e., eu não "dei enter" após a última letra da última linha.

É prática comum terminar todas as linhas com \n, tanto que muitas vezes esse caractere é chamado de caractere de fim de linha. Sempre adicione um caractere de fim de linha no final do seus arquivos de texto.

Observe também que nome_completo começa com um espaço, assim como há alguns espaços no final de nascimento. Isso porque quando copiei o arquivo em meu editor de texto adicionei alguns arquivos em branco. Muitas vezes não vemos esses caracteres, então eles passam desapercebidos. É uma boa prática não deixar esses caracteres no final das linhas de seus arquivos de texto. Descubra como configurar seu editor de texto.

Acontece que quando criamos um programa, não temos controle sobre os arquivos que leremos. Então o que a maioria das programadoras faz é livrar-se desses caracteres em branco. As strings em Python têm um função para isso, strip:

>>> nome_completo.strip()
'Ana Viva Mariana'

Pode ser que você queira ler as linhas de um arquivo, mas não conheça quantas linhas deverá ler até que o arquivo termine. Para isso, Python permite percorrer as linhas do arquivo como se ele fosse uma lista de strings — com a diferença crucial de que não podemos voltar nem acessar uma linha com colchetes. Já podemos ler nosso arquivo de palavras.

def ler_aquivo_palavras(nome_arquivo):
    """
    Lê um arquivo e devolve a lista de palavras,
    uma por linha
    """

    with open(nome_arquivo) as arquivo:
        palavras = []
        for linha in arquivo:
            palavra = linha.strip()
            palavras.append(palavra)

    return palavras

Agora já podemos criar duas listas separadas, uma com as palavras "plurais" e outras com as palavras "singulares" (é claro que isso não é correto gramaticalmente, decidir se uma palavra está em plural é muito mais desafiador do que simplesmente verificar se a última letra é um "s").

def separar_plurais(palavras):
    """
    Devolve a lista das palavras que terminam em s
    """
    plurais = []
    for palavra in palavras:
        if palavra[-1] == "s":
            plurais.append(palavra)
    return plurais

def calcular_diferenca(lista1, lista2):
    """
    Devolve uma lista com os elementos
    de lista1 que não estão em lista2
    """
    diferenca = []
    for valor in lista1:
        if valor not in lista2:
            diferenca.append(valor)
    return diferenca

def main():
    palavras = ler_aquivo_palavras("palavras.txt")
    plurais = separar_plurais(palavras)
    singulares = calcular_diferenca(palavras, plurais)

    print(plurais)
    print(singulares)

    # criar_arquivo_palavras("plural.txt", plurais)
    # criar_arquivo_palavras("singular.txt", singulares)

main()

Isso deve ser suficiente para testar a leitura do arquivo. Experimente com o arquivo seguinte.

feijão
arroz
limões
batata
beterrabas
pizzas
lasanha quatro-queijos
rapadura

Escrevendo dados em um arquivo

Para completar o nosso exercício, precisamos implementar a função criar_arquivo_palavras(nome_arquivo, palavras), cujas chamadas estão comentadas no trecho acima. O que essa função deve fazer é:

1. criar um arquivo chamado nome_arquivo;
2. escrever as palavras no arquivo, uma por linha.

Quando chamamos open("palavras.txt") acima, abrimos esse arquivo no chamado modo de leitura. Para poder escrever em um arquivo, precisamos abrir um aquivo no modo de escrita. Para isso faremos algo como open("plurais.txt", "w"). Esse caractere "w" está indicando que o mode abertura do arquivo é de leitura. Quando não passamos esse parâmetro, o padrão é modo de leitura, que também pode ser indicado pelo caractere "r". Dependendo do objetivo, existem vários modos de abertura de um arquivo, como os do exemplo abaixo. Mas os modos "r" e "w" são os mais comuns.

modo	operações	posição do cursor do arquivo
"r"	leitura	início
"r+"	leitura e escrita	início
"w"	escrita	início (trunca arquivo)
"w+"	escrita e leitura	início (trunca arquivo)
"a"	escrita	final
"a+"	leitura	início

O modo que iremos usar para nossa função é o "w", o que esse modo significa é o seguinte:

1. se o arquivo sendo aberto não existir, então um aquivo com esse nome é criado;
2. se um arquivo com esse nome existir, então esse arquivo é truncado a 0 bytes, descartando quaisquer dados armazenados anteriormente;
3. o cursor de arquivo é posicionado em modo de escrita no início do arquivo, que nesse momento está vazio.

Tome cuidado ao usar o modo de escrita "w", já que ele pode levar a perda de dados. Pode ser necessário verificar se o arquivo já existe, ou renomeá-lo se já existir. Para isso, procure no módulo os as funções adequadas, como os.rename ou os.remove.

Para entender o significado de cada modo disponível, consulte a documentação de open. Aqui, só precisamos escrever uma linha por vez. Fazemos isso com a função write, que está disponível para os arquivos.

def criar_arquivo_palavras(nome_arquivo, palavras):
    """
    Cria um arquivo nome_arquivo com as palavras,
    uma por linha
    """

    with open(nome_arquivo, "w") as arquivo:
        for palavra in palavras:
            linha = palavra + "\n"
            arquivo.write(linha)

Repare que para escrever uma linha, precisamos adicionar uma quebra de linha no final de cada linha manualmente. Se não fizermos isso, então todas as palavras apareceriam coladas. Se preferir, também é possível utilizar a função print, que irá escrever no arquivo da mesma maneira que escreveria na tela. A vantagem é que print converte a variável para uma string automaticamente.

>>> lista = [1, 2, 3]
>>> with open("lista.txt", "w") as arquivo:
...     print(lista, file=arquivo)

Experimente e descubra qual o conteúdo foi criado no arquivo "lista.txt".

Entrada e saída padrão

Quando vimos como abrir arquivos, aprendemos que uma variável do tipo arquivo tem uma função fileno que devolve um descritor do arquivo, que é um número que designa um arquivo aberto de seu programa para o sistema operacional. Se você executou o exemplo, é muito provável que arquivo.fileno() devolveu o mesmo número 3 mostrado acima. Mas por que o primeiro arquivo que abrimos tem descritor 3, e não 0 ou 1?

A resposta é que quando nossas instruções começam a executar, o processo associado a nosso programa já tem três arquivos abertos. Esses arquivos podem ser acessados a partir do módulo sys, i.e, se escrevermos import sys no início do programa. São eles:

• A entrada padrão sys.stdin, que tem descritor 0. Esse arquivo começa aberto no modo de leitura e representa os dados digitados pelo usuário. Normalmente acessamos esse arquivo através da função input.
• A entrada padrão sys.stdout, que tem descritor 1. Esse arquivo começa aberto no modo de escrita e representa os dados mostrados na tela. Normalmente acessamos esse arquivo através da função print.
• A entrada padrão sys.stderr, que tem descritor 2. Esse arquivo começa aberto no modo de escrita e representa as mensagens de erro mostradas na tela. Normalmente acessamos esse arquivo através da função print, mas passando o parâmetro file=sys.stderr.

Nesta disciplina não usamos ainda mensagens de erro, mas elas podem ser úteis para distinguir a saída do seu programa de uma mensagem, particularmente uma mensagem de quando estamos testando o nosso programa.

Entender e conhecer os arquivos de entrada e saída padrão é bastante conveniente, particularmente quando nos cansarmos de testar nossos programas digitando a entrada na mão, de novo e de novo. Em um terminal podemos escrever

user@notebook$ python3 programa.py < entrada.txt > saida.txt

Isso irá fazer com que sys.stdin se refira ao arquivo entrada.txt e sys.stdout se refira ao arquivo saida.txt. Se também quisermos guardar as mensagens de erro, poderíamos escrever

user@notebook$ python3 programa.py < entrada.txt > saida.txt 2> erros.txt

mas é útil deixar que as mensagens de erro sejam mostradas na tela. Vamos fazer isso em breve.

Um exemplo com matrizes

Vamos resolver o seguinte exercício:

Escreva um programa que dada uma matriz de caracteres e uma palavra, conte o número de vezes que a palavra aparece na matriz, tanto na direção vertical quanto na horizontal.

Vamos ver um exemplo.

OEAIAGBOOL
IIWAXHHLHN
PADUCAPNOC
ZBMOUIZSAS
OXEZOKOEUA
QCRMAAPAOH
DHOMEMTUFO
HOOAJCMVGM
NMFOANGMAE
JEVJVCCSNM

Se estivermos procurando HOMEM, você deve encontrar duas ocorrências dessa palavra na matriz acima.

Antes de tudo, precisamos formalizar o problema que nos é dado. O enunciado não fala de onde essa matriz será obtida, nem de onde vamos ler a palavra. Não é razoável digitar toda a matriz sempre que formos testar nosso programa — acho que você deve concordar comigo, então não devemos sequer cogitar testar esse programa digitando a entrada.

A solução agora deve ser evidente: vamos criar um arquivo para armazenar a entrada de nosso programa. Nossa entrada é uma matriz de caracteres e uma palavra, então é natural utilizarmos um arquivo de texto. Precisamos de alguma convenção para organizar os dados no nosso arquivo, assim definiremos a seguinte estrutura do arquivo, bem simples:

• a primeira linha contém a palavra sendo buscada;
• as demais linhas contém as linhas da matriz, sem espaço entre os caracteres.

Vamos criar um arquivo chamado caca_palavras.txt.

HOMEM
OEAIAGBOOL
IIWAXHHLHN
PADUCAPNOC
ZBMOUIZSAS
OXEZOKOEUA
QCRMAAPAOH
DHOMEMTUFO
HOOAJCMVGM
NMFOANGMAE
JEVJVCCSNM

Enquanto esse exercício não é difícil, ele tampouco é trivial. Assim, precisamos de método e organização, senão iremos gastar muito tempo tentando resolvê-lo e a experiência de programação será frustrante. Como sempre, vamos fazer uma lista de funções a serem implementadas e, para cada uma delas, escrever um algoritmo em português antes de programá-la. Precisamos de pelo menos duas funções, com os seguintes objetivos:

1. ler um arquivo e devolver uma palavra e a matriz de caracteres;
2. procurar uma ocorrência de uma palavra na matriz.

A primeira tarefa é mecânica: basta ler a primeira linha e depois percorrer as demais linhas adicionado as palavras a uma lista.

def ler_arquivo_entrada(nome_arquivo):
    """Lê um arquivo com os dados de entrada
    e devolve a palavra e a matriz de caracteres"""

    with open(nome_arquivo) as arquivo:
        palavra = arquivo.readline().strip()
        matriz = []
        for linha in arquivo:
            matriz.append(linha.strip())
    return palavra, matriz

Representamos uma matriz de caracteres como uma lista de strings! Assim, podemos acessar um caractere na linha i e coluna j normalmente, digitando matriz[i][j]. Enquanto isso é conveniente, há uma consequência em termos de desempenho. Para acessar um elemento de uma lista em uma posição j dada, o interpretador Python pode acessar essa posição na memória diretamente, isso é muito muito rápido.

Já para acessar um caractere de uma string em uma dada posição j, é necessário percorrer toda a string desde o início contando os caracteres. Para strings pequenas como do nosso exemplo isso não é um problema, mas para strings maiores ou para aplicações críticas, isso pode ser extremamente ineficiente. Por sorte, é fácil corrigir esse problema, basta converter a string em uma lista, mudando a iteração do for para matriz.append(list(linha.strip())). Sutil, mas importante!

Para a segunda tarefa, queremos procurar as ocorrências de uma palavra na matriz. Um algoritmo em alto nível, que é talvez o que a maioria das pessoas faria, é o seguinte:

• para cada linha $i$ da matriz
  • para cada coluna $j$ da matriz
    1. verifique se a palavra aparece horizontalmente a partir de $(i,j)$
    2. verifique se a palavra aparece verticalmente a partir de $(i,j)$
    3. atualize o contador de ocorrências

Agora escrevemos a função. Vamos postergar as tarefas mais difíceis usando stubs.

def contar_ocorrencias(palavra, matriz):
    """Conta o número de vezes que palavra
    ocorre em matriz, horizontal ou verticalmente"""

    m = len(matriz)
    n = len(matriz[0])

    ocorrencias = 0
    for i in range(m):
        for j in range(n):
            if ocorre_horizontal(palavra, matriz, i, j):
                ocorrencias += 1
            if ocorre_vertical(palavra, matriz, i, j):
                ocorrencias += 1

    return ocorrencias

Essa função não morde. Vamos passar à função main.

def main():
    palavra, matriz = ler_arquivo_entrada("caca_palavras.txt")
    ocorrencias = contar_ocorrencias(palavra, matriz)
    print(f"Há {ocorrencias} ocorrencias")

A mágica realmente acontece quando procuramos a ocorrência de uma palavra. Vamos implementar ocorre_vertical. Um algoritmo seria o seguinte:

1. $ocorre \gets True$
2. para cada índice $k$ de $palavra$:
   • compare os caracteres $palavra[k]$ com $matriz[i][j + k]$
   • se forem diferentes, faça $ocorre \gets False$
3. devolva $ocorre$

Isso verifica se cada caractere de palavra é corresponde a algum caractere na linha $i$ da matriz começando pela coluna $j$.

def ocorre_horizontal(palavra, matriz, i, j):
    ocorre = True
    tamanho = len(palavra)
    for k in range(tamanho):
        if palavra[k] != matriz[i][j + k]:
            ocorre = False
    return ocorre

def ocorre_vertical(palavra, matriz, i, j):
    return False

Juntamos todas as partes e executamos o nosso programa, digamos caca_palavras.py, apenas para descobrir que ele tem um erro.

user@notebook:~/ra123456/matrizes$ python3 caca_palavras.py
Traceback (most recent call last):
  File "caca_palavras.py", line 46, in <module>
    main()
  File "caca_palavras.py", line 43, in main
    ocorrencias = contar_ocorrencias(palavra, matriz)
  File "caca_palavras.py", line 22, in contar_ocorrencias
    if ocorre_horizontal(palavra, matriz, i, j):
  File "caca_palavras.py", line 33, in ocorre_horizontal
    if palavra[k] != matriz[i][j + k]:
IndexError: list index out of range

Existe um erro ao acessar a coluna $j+k$ da linha $i$ da matriz. Para poder corrigir esse erro, utilizamos um debugger, possivelmente colocando configurando breakpoint na linha em que aconteceu o erro, ou um pouco antes. Muitas vezes, é útil também colocar alguma mensagem de debug. Para distinguir a mensagem de debug da saída normal do nosso programa, vamos escrever no arquivo sys.stderr, que é para onde esse tipo de mensagem deve ir.

import sys

# ...

def ocorre_horizontal(palavra, matriz, i, j):
    ocorre = True
    tamanho = len(palavra)
    for k in range(tamanho):
        print(f"Comparando palavra[{k}] com matriz[{i}][{j + k}]", file=sys.stderr)
        if palavra[k] == matriz[i][j + k]:
            ocorre = False
    return ocorre

Executando novamente, temos um bocado de informação na tela, resumida a seguir:

user@notebook:~/ra123456/matrizes$ python3 caca_palavras.py
Comparando palavra[0] com matriz[0][0]
Comparando palavra[1] com matriz[0][1]
Comparando palavra[2] com matriz[0][2]
....
Comparando palavra[0] com matriz[0][6]
Comparando palavra[1] com matriz[0][7]
Comparando palavra[2] com matriz[0][8]
Comparando palavra[3] com matriz[0][9]
Comparando palavra[4] com matriz[0][10]
Traceback (most recent call last):
  File "caca_palavras.py", line 49, in <module>
    main()
  File "caca_palavras.py", line 46, in main
    ocorrencias = contar_ocorrencias(palavra, matriz)
  File "caca_palavras.py", line 24, in contar_ocorrencias
    if ocorre_horizontal(palavra, matriz, i, j):
  File "caca_palavras.py", line 36, in ocorre_horizontal
    if palavra[k] != matriz[i][j + k]:
IndexError: list index out of range

Se você contar, irá descobrir que a matriz tem apenas 10 colunas, mas matriz[0][10] se refere à décima-primeira coluna da primeira linha, que não existe. Encontramos o erro. A vantagem de mostrar mensagens de debug na saída de erro é que, enquanto escrevemos o programa, podemos omitir essas mensagens, sem precisar remover as instruções do código. Depois de modificada a função para tentar corrigir o erro, fazemos o seguinte:

user@notebook:~/ra123456/matrizes$ python3 caca_palavras.py 2> /dev/null
Há 1 ocorrencias

Vemos somente a saída padrão. Nesse caso, eu executei o programa depois de corrigir a função ocorre_horizontal. Corrija essa função e implemente a função que falta.