PageRank

Uma página Web pode ser considerada relevante por uma máquina de busca se várias páginas apontam para ela e/ou se ela é referenciada por outras páginas relevantes. Este é o princípio por trás da métrica PageRank, desenvolvida pela universidade de Stanford e utilizada, com variações, pelo Google.

Nesta tarefa, trabalharemos com uma estrutura simplificada da Web em que teremos apenas informações sobre identificadores de páginas e links. As páginas serão identificadas por letras e um link de uma página A para uma página B será indicado por A -> B. Os cálculos dos valores de PageRank serão feitos de maneira iterativa.

Valor inicial: O valor inicial PR0(id_pag) é $1/N$, onde N é o número de identificadores das páginas na rede.

Fator de amortecimento: o algoritmo estabelece um valor d para indicar a probabilidade de um usuário seguir um link a partir da página atual ao invés de digitar um novo endereço Web no navegador. O fator de amortecimento garante que páginas sem nenhum link para elas possam ter uma probabilidade mínima $(1-d)/N$ de acesso. Nesta tarefa, adotaremos d = 0.875 para todos os exemplos e testes.

Número de links: O número de links de saída uma página N_Links(id_pag) reflete o número de páginas distintas apontadas por id_pag. Para o cálculo do PageRank, links de uma página para ela mesma serão desconsiderados. Em caso de múltiplos links de uma página para outra, apenas o primeiro será considerado.

Passo: O valor de PageRank de uma página no passo i (PRi(id_pag)) será calculado a partir dos valores PRi-1 das páginas id_pag_link que apontam para id_pag de acordo com a fórmula abaixo:

$PR$i(id_pag) = (1 - d)/N + d * ∑ PRi-1(id_pag_link)/N_Links(id_pag_link)  

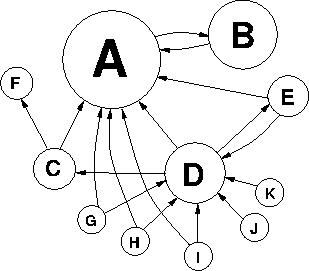
Exemplo: Observe na tabela abaixo os links e a rede que representam a figura ilustrativa da tarefa, os valores iniciais de PageRank, os valores do primeiro passo e os valores estáveis:

Links	Rede	PageRank Inicial	PageRank Passo 1	...	PageRank Final
A -> B B -> A C -> A C -> F D -> A D -> C D -> E E -> A E -> D G -> A G -> D H -> A H -> D I -> A I -> D J -> D K -> D		A: 0.091 B: 0.091 C: 0.091 D: 0.091 E: 0.091 F: 0.091 G: 0.091 H: 0.091 I: 0.091 J: 0.091 K: 0.091	A: 0.316 B: 0.091 C: 0.038 D: 0.330 E: 0.038 F: 0.051 G: 0.011 H: 0.011 I: 0.011 J: 0.011 K: 0.011		A: 0.333 B: 0.304 C: 0.028 D: 0.059 E: 0.028 F: 0.024 G: 0.011 H: 0.011 I: 0.011 J: 0.011 K: 0.011

Considerando ainda o exemplo acima, podemos analisar como foi feito o cálculo de PR1(A):

Páginas que apontam para A: B C D E G H I
    
PR1(A) = (1 - d)/N + d * (PR0(B)/N_links(B) + PR0(C)/N_links(C) +
      PR0(D)/N_links(D) + PR0(E)/N_links(E) + PR0(G)/N_links(G) + 
      PR0(H)/N_links(H) + PR0(I)/N_links(I))
    
N = 11
d = 0.875
PR0(B) = PR0(C) = PR0(D) = PR0(E) = PR0(G) = PR0(H) = PR0(I) = 0.091
N_links(B) = 1
N_links(C) = N_links(E) = N_links(G) = N_links(H) = N_links(I) = 2    
N_links(D) = 3

PR1(A) = (1 - 0.875)/11 + 0.875 * (0.091/1 + 0.091/2 +
      0.091/3 + 0.091/2 + 0.091/2 + 
      0.091/2 + 0.091/2) = 0.316

Número de passos: Podemos determinar se os valores estabilizaram verificando se as variações de PageRank de um passo para outro são nulas ou mínimas. Nesta tarefa, não iremos adotar esta abordagem, mas sim efetuar um número pré-estabelecido de passos.

Descrição da entrada

A primeira linha conterá a lista de identificadores de páginas, separados por espaços em branco. As linhas seguintes conterão zero ou mais links no formato indicado e a última linha conterá o número de passos a serem calculados. O esquema geral está descrito abaixo:

<id_pag1> <id_pag2> ... <id_pagn>
<id_pag_orig1> -> <id_pag_dest1>
<id_pag_orig2> -> <id_pag_dest2>
...
<id_pag_origm> -> <id_pag_destm>
<num_passos>

Um exemplo com quatro páginas, quatro links e dois passos seria:

A B C D 
A -> B
B -> C
B -> D
C -> D
2

Descrição da saída

A primeira parte da saída descreverá as ligações entre as páginas de maneira resumida. Para cada página com identificador <id_pag>, em ordem alfabética, será gerado um par de linhas no formato abaixo. A primeira linha contém o identificador <id_pag>, o símbolo -> e a lista de páginas para as quais <id_pag> aponta. A segunda linha contém a lista de páginas que apontam para <id_pag>, o símbolo -> e o identificador <id_pag>. Note que na apresentação destas listas não devem aparecer múliplos links nem links de uma página para ela mesma.

<id_pag> -> [ ]
[ ] -> <id_pag>      

A segunda parte conterá os valores de PageRank calculados para cada passo do algoritmo. As páginas deverão aparecer em ordem alfabética e os valores de PageRank formatados com três casas decimais.

PageRank (passo <i>)
<id_pag1>: <PRi(<id_pag1)>
<id_pag2>: <PRi(<id_pag2)>
...

Para o exemplo da seção anterior, a saída será:

A -> ['B']
[] -> A
B -> ['C', 'D']
['A'] -> B
C -> ['D']
['B'] -> C
D -> []
['B', 'C'] -> D
PageRank (passo 0)
A: 0.250
B: 0.250
C: 0.250
D: 0.250
PageRank (passo 1)
A: 0.031
B: 0.250
C: 0.141
D: 0.359
PageRank (passo 2)
A: 0.031
B: 0.059
C: 0.141
D: 0.264

Testes com o SuSy

O conjunto de testes será formado por nove testes abertos e um teste fechado. A tabela abaixo mostra detalhadamente os quatro primeiros testes abertos.

Teste	Links Entrada	Rede	Lista Links	PageRank
arq1.in			A -> [] [] -> A B -> [] [] -> B	PageRank (passo 0) A: 0.500 B: 0.500 PageRank (passo 1) A: 0.062 B: 0.062
arq2.in	A -> B		A -> ['B'] [] -> A B -> [] ['A'] -> B	PageRank (passo 0) A: 0.500 B: 0.500 PageRank (passo 1) A: 0.062 B: 0.500 PageRank (passo 2) A: 0.062 B: 0.117
arq3.in	A -> B B -> A		A -> ['B'] ['B'] -> A B -> ['A'] ['A'] -> B	PageRank (passo 0) A: 0.500 B: 0.500 PageRank (passo 1) A: 0.500 B: 0.500
arq4.in	A -> B C -> B		A -> ['B'] [] -> A B -> [] ['A', 'C'] -> B C -> ['B'] [] -> C	PageRank (passo 0) A: 0.333 B: 0.333 C: 0.333 PageRank (passo 1) PageRank (passo 1) A: 0.042 B: 0.625 C: 0.042 PageRank (passo 2) A: 0.042 B: 0.115 C: 0.042

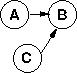
Releia, se necessário, as instruções para fazer os testes em Testes com o SuSy.

Orientações para submissão

Veja aqui a página de submissão da tarefa. O arquivo a ser submetido deve se chamar lab10.py. No link Arquivos auxiliares há um arquivo aux10.zip que contém todos os arquivos de testes abertos e seus respectivos resultados compactados.

O limite máximo será de 20 submissões. Serão considerados os resultados da última submissão.

O peso desta tarefa é 4.

O prazo final para submissão é 17/11/2019.

A nota desta tarefa é proporcional ao número de testes que executaram corretamente, desde que o código esteja coerente com o enunciado. A submissão de um código que não implementa o algoritmo requisitado, mas que exibe as saídas esperadas dos testes abertos a partir da comparação de trechos da entrada será considerada fraude e acarretará a atribuição de nota zero à média final da disciplina.