Ata

Ata – Capítulo 34 – Problemas NP-Completos II

Aula dia 18/06/2003

Redatora: Daniele Constant Guimarães

Ra: 012108

Tópicos:

1. Introdução

2. Algoritmos de Verificação: Exemplos

2.1. Descrição

2.2. Discussão em aula

3. Classes NP e co-NP

3.1. Descrição

3.2. Discussão em aula

4. Redutibilidade: algoritmo de redução, função de redução, linguagem redutível a outra.

4.1. Descrição

4.2. Discussão em aula

5. A classe NPC (linguagens NP completas)

5.1. Descrição

5.2. Discussão em aula

6. Um problema NP completo: satisfabilidade de circuitos, CIRCUIT-SAT

6.1. Descrição

6.2. Discussão em aula

7. Redução de CIRCUIT-SAT a SAT

7.1. Descrição

7.2. Discussão em aula

8. Conclusão

Os tópicos acima foram discutidos em ordem. O professor coordenou a discussão fazendo uma pergunta para cada aluno e propondo itens a serem discutidos. Ele iniciou a aula fazendo um breve resumo dos conceitos da aula anterior, pois estes eram importantes para esta aula. E em seguida foi solicitado que o professor revisasse o exemplo que faz analogia de algoritmos com tabelas.

1. Introdução

Neste capítulo foi discutida a classe de problemas NP-completos, cujo status é desconhecido. Ainda não foi descoberto nenhum algoritmo de tempo polinomial para resolver os problemas que se encaixam nesta classe, nem foi provado que não pode existir nenhum algoritmo de tempo polinomial que os resolva.

Na aula anterior foram discutidos os conceitos básicos sobre NP-Completude. Foi visto como transformar a maioria dos problemas de otimização, incluindo todos os que foram vistos no curso, em problemas de decisão, que são definidos da seguinte forma: existe um conjunto de strings {0, 1}. Dada uma string, ela pertence ou não a esse conjunto?

Todos os problemas, de uma forma mais ou menos padronizada, foram resolvidos reduzidos a esse tipo de problema.

Foi visto também o conceito de redução, que consiste em transformar uma instância de um problema A em uma instância de um problema B. Essa transformação deve ser feita em tempo polinomial e as respostas para os problemas devem ser as mesmas, ou seja, a resposta para a instância de A é, por exemplo, “sim” se e somente se a resposta para a instância de B é “sim”.

2. Algoritmos de Verificação: Exemplos

2.1. Descrição

Um algoritmo de verificação é definido como um algoritmo A que recebe como entrada dois argumentos, sendo um deles uma cadeia de entrada x e o outro uma cadeia binária y, chamada de certificado. Esse algoritmo verifica a cadeia de entrada x se existe um certificado y tal que A(x,y) = 1. A linguagem verificada por um algoritmo de verificação A é dada por: L={x ∈ {0,1}^*: existe y ∈ {0,1}^* tal que A(x,y)=1}.

Em outras palavras, um algoritmo A verifica uma linguagem L se, para qualquer cadeia x ∈ L, existe um certificado y que A pode utilizar para provar que x ∈ L. E, para qualquer cadeia x ∈ L, não deve haver nenhum certificado provando que x ∈ L.

Exemplo: Dado um grafo G hamiltoniano e os vértices em ordem ao longo do ciclo hamiltoniano. Para verificar que o ciclo dado é realmente hamiltoniano, basta verificar se ele é uma permutação dos vértices de V e se cada uma das arestas consecutivas ao longo do ciclo realmente existe no grafo. A lista dos vértices de V, nesse caso, é o certificado.

2.2. Discussão em aula

O professor iniciou pedindo a um dos alunos que falasse sobre a definição de algoritmo de verificação e em seguida desse um exemplo. O professor encerrou este tópico esclarecendo algumas dúvidas.

Algoritmo de verificação é um algoritmo que aceita dois argumentos (uma cadeia de entrada – x – e um certificado – y).

Ex: Problema dos ciclos hamiltonianos. O algoritmo recebe um grafo (cadeia de entrada) e uma lista ordenada de vértices como uma cadeia de verificação (certificado). Ele testa se existem arestas entre os vértices da cadeia de verificação (entre o 1º e o 2º, 2º e 3º...) e verifica se ela é uma permutação dos vértices do grafo. Se for e existir uma aresta entre os vértices consecutivos da cadeia de verificação, então ela é uma solução para o problema.

Nesse ponto foram esclarecidas algumas dúvidas, pelo professor, com relação à terminologia usada.

· x é uma instância para o problema

· Certificado (y) é um sinônimo para solução

Resumindo, um algoritmo de verificação recebe uma instância do problema e uma solução ou uma pretensa solução como entrada e seu objetivo é verificar se essa instância é uma solução para o problema. Verificar essa solução é fácil, o difícil é encontrá-la.

O termo certificado é usado porque, sendo um problema de decisão, ele assegura que a resposta é correta. No caso do problema do ciclo hamiltoniano o algoritmo recebe um grafo e não sabe se o grafo tem ou não um ciclo hamiltoniano. Se for apresentado um certificado e a solução for facilmente verificável, então o grafo tem um ciclo hamiltoniano. Nesse caso, a solução é facilmente verificável, dado um ciclo hamiltoniano, basta verificar se os vértices consecutivos têm uma aresta entre eles.

Existem problemas para os quais ainda não foi possível encontrar um certificado sucinto e verificável em curto espaço de tempo e não é fácil encontrá-los.

3. Classes NP e co-NP

3.1. Descrição

A classe de complexidade NP é a classe de linguagens que podem ser verificadas por um algoritmo de tempo polinomial. A partir dessa definição, pode-se dizer que se uma linguagem L ∈ P então L ∈ NP, pois se existe um algoritmo de tempo polinomial para decidir L, ele pode ser convertido em um algoritmo de verificação de dois argumentos. Logo, P ⊂ NP. Mas, não se sabe se P = NP.

A classe de complexidade co-NP é definida como sendo o conjunto de linguagens L tais que ∈ NP.

Mas, não se sabe qual a relação entre essas classes. Existem 4 possibilidades que estão ilustradas abaixo:

(a)

(b)

(c)

(d)

Figura 1: As quatro possibilidades de relacionamentos entre as classes de complexidade. (a)P=NP=co-NP. A maioria dos pesquisadores considera essa possibilidade a mais improvável. (b) se NP é fechada sob o complemento, então NP=co-NP, mas não é preciso haver P=NP. (c) NP ∩ co-NP = P, mas NP não é fechada sob o complemento. (d) NP ≠ co-NP e NP ∩ co-NP ≠ P. A maioria dos pesquisadores considera essa possibilidade a mais provável.

3.2. Discussão em aula

Este tópico foi iniciado com as definições de classes NP e co-NP.

A classe NP é a classe de linguagens que podem ser verificadas em tempo polinomial por um algoritmo de verificação.

A classe co-NP é a classe complementar, ou seja, dada uma linguagem que está em co-NP, seu complemento está em NP.

Eles não sabem como enquadrar a classe de complexidade co-NP. Eles não sabem se P=NP=co-NP, se NP=co-NP e P ≠ NP, se NP ≠ co-NP e P=NP ∩ co-NP ou se NP ≠ co-NP e P ≠ (NP ∩ co-NP) (ver a Figura 1 acima)

A partir desse ponto, o professor esclareceu as dúvidas dos alunos.

Para esclarecer a seguinte dúvida “Se não se sabe se a classe co-NP=NP, então não se sabe se ela pode ser verificada em tempo polinomial?” o professor usou o exemplo de números primos:

Seja dado o conjunto dos números primos. Existe um certificado curto que possa ser dado que convença que um determinado número não é primo? Pensando ao contrário, se um número não é primo, ele é composto. Existe algum certificado curto que possa ser dado que convença que aquele número é composto? Nesse caso, é só mostrar um divisor.

Moral da história: o conjunto dos números primos está em co-NP, porque seu complemento, que é o conjunto dos números compostos, é fácil de verificar.

Falando ainda sobre a classe complementar, a questão do complemento não existe para problemas polinomiais porque seu complemento é obviamente polinomial também. É só pegar uma instância, testar se ela está no conjunto, a resposta obtida é sim ou não. Depois é só inverter a resposta e devolver. Então o algoritmo polinomial para um problema e o algoritmo para o seu complemento é praticamente o mesmo, mudando apenas o final.

Quando se fala em NP, ou seja, verificabilidade de tempo polinomial, o algoritmo não se transfere automaticamente para o complemento. O fato de saber verificar polinomialmente se uma cadeia (string) pertence a uma linguagem, não significa que exista uma maneira direta para encontrar o certificado para o complemento.

É o caso dos números primos, por exemplo. Existe um certificado pra saber se um número não é primo, agora o certificado para saber se ele é primo é muito mais complicado.

Outro exemplo é o problema do ciclo hamiltoniano. É fácil apresentar um certificado de que um grafo tem um ciclo hamiltoniano. É só mostrar o ciclo e verificá-lo. Se o ciclo dado como certificado não for hamiltoniano, não se pode dizer que o grafo não é hamiltoniano. Pois pode existir um outro certificado que diga que o grafo é hamiltoniano. Se todos os ciclos fossem dados, seria considerado um certificado, mas nesse caso, ele não seria verificável em tempo polinomial.

Sobre os números primos: foi provado há pouco tempo, que o conjunto dos números primos está em P. Na década de 70/80 foi demonstrado que o conjunto dos números primos está em NP. Ou seja, não é óbvio, mas existem certificados polinomiais que dão certeza que um número é primo, o que fez com que o conjunto dos números primos ficasse conhecido como um problema da interseção NP ∩ co-NP. Ainda não se sabe se ele é um problema NP-completo. Para provar que ele é NP-completo, deve-se provar que um outro problema NP-completo é redutível a ele.

4. Redutibilidade: algoritmo de redução, função de redução, linguagem redutível a outra.

4.1. Descrição

A redutibilidade em tempo polinomial é usada para comparar a “dificuldade” relativa entre linguagens. Um problema Q pode ser reduzido a outro problema Q’ se qualquer instância de Q pode ser reformulada como uma instância de Q’, cuja solução fornece uma solução para a instância de Q.

Uma linguagem L₁ é redutível em tempo polinomial a uma linguagem L₂ (L₁ L₂), se existe uma função de tempo polinomial f: {0,1}^* → {0,1}^* para todo x ∈ {0,1}^*, tal que: x ∈ L₁ se e somente se f(x) ∈ L₂. Essa função f é chamada de função de redução e um algoritmo de tempo polinomial F que calcula f é chamado de algoritmo de redução.

Se L₁ L₂, significa dizer que L₁ não é mais que um fator polinomial mais difícil que L₂.

4.2. Discussão em aula

O professor iniciou esse tópico perguntando as definições algoritmos e funções de redução.

Uma função de redução é uma função que, dado um problema Q torna possível reformulá-lo para um outro problema Q’. Dessa forma, resolvendo um problema, resolve-se também o outro. Se essa função for calculada em tempo polinomial e o problema Q’ puder ser resolvido em tempo polinomial, então o problema Q também será resolvido em tempo polinomial. A mesma função pode ser calculada por diversos algoritmos.

Um algoritmo de redução é um algoritmo que calcula a função de redução em tempo polinomial

A função de redução deve ter a seguinte propriedade essencial:

Dada uma string x qualquer, x ∈ L₁ se e somente se f(x) ∈ L₂. Dito de outra forma, se x ∈ L₁ então f(x) ∈ L₂, e se f(x) ∈ L₂, então x ∈ L₁. Essa função não precisa ser bijetora, pois podem existir elementos em L₂ que não tenham correspondentes em L₁, ou seja, ninguém chega nele e podem existir também dois elementos em L₁ que chegam no mesmo elemento de L₂.

Para exemplificar a questão da não bijeção da função, o professor usou o problema do ciclo hamiltoniano:

Restrinja o problema do ciclo hamiltoniano a grafos onde todos os vértices tenham grau menor ou igual a três. Esse é um grafo esparso. Suponha também, que o problema de procurar ciclos hamiltonianos em grafos de grau no máximo 3 seja NP-completo. Nesse caso, pode-se fazer uma redução do problema geral.

Por enquanto, sabemos que o problema do ciclo hamiltoniano é NP, não sabemos se ele é NP-completo, mas se o problema restrito a grau 3 for NP-completo, então o problema geral também será. Isso é possível porque se existe uma solução para todos os grafos, existe uma solução para grafos com grau no máximo 3. Se não é possível resolver para grafos com grau no máximo 3, não será possível resolver para os gerais.

A redução, nesse caso, só ocupa uma parte do domínio. Ou seja, vários elementos da linguagem L₂ (grafos com grau maior que 3) não foram tocados pela função.

O próximo item a ser levantado pelo professor foi: “Intuitivamente, o que significa a redução?”.

Intuitivamente, redução significa conseguir mostrar que um problema é mais fácil ou igual ao outro. Igual, a menos de um fator polinomial.

Nesse ponto o professor esclareceu as dúvidas quanto à interpretação do significado da notação L₁L₂, que está no livro texto adotado na página 778, na sessão “Problemas NP-completos”.

No livro diz: “... se L₁L₂, então L₁ não é mais que um fator polinomial mais difícil que L₂ ...”.

O professor interpretou da seguinte forma: “Significa que L₁ pode ser mais difícil que L₂ apenas por um fator polinomial. Ou seja, o fator polinomial aqui é considerado ‘nada’ (desprezível), então, quer dizer que L₁ não pode ser mais difícil que L₂. Agora, em redução, por outro lado, L₂ pode ser bem mais difícil que L₁ e essa notação continua valendo”.

Para que L₁e L₂ tivessem a mesma complexidade, a redução deveria ser feita dos dois lados: L₁L₂ e L₂L₁.

5. A classe NPC (linguagens NP-completas)

5.1. Descrição

O conjunto de linguagens NP-completas (NPC) contém os problemas mais difíceis em NP. Uma linguagem L ∈ {0,1}^*é NP-completa se satisfizer duas condições:

1. L ∈ NP

2. L’ L para todo L’ ∈ NP

Essa última condição diz que toda linguagem que pertence à classe NP é redutível em tempo polinomial a L.

Uma linguagem L é NP-difícil se ela satisfizer a propriedade 2, mas não necessariamente satisfizer a propriedade 1.

Existe um teorema que diz: “Se qualquer problema NPC puder ser resolvido em tempo polinomial, então P=NP. Se qualquer problema em NP não pode ser resolvido em tempo polinomial, então nenhum problema NPC pode ser resolvido em tempo polinomial”.

Figura 2: Esse é o modo como a maioria dos cientistas da computação teórica vê os relacionamentos entre P, NP e NPC. Tanto P quanto NPC estão inteiramente contidas dentro de NP, e P ∩ NPC = ∅ .

5.2. Discussão em aula

Para iniciar este tópico foi solicitado a um aluno que definisse as classes NPC e NP-difícil.

Uma linguagem L é NPC se satisfizer 2 condições:

1. L ∈ NP

2. L’ L para todo L’ ∈ NP

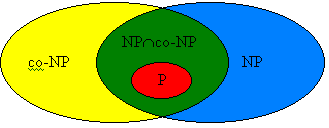
Uma linguagem L é NP-difícil se ela satisfizer a segunda condição, mas não necessariamente satisfizer a primeira. NP-difícil também é uma classe de complexidade. Nem todo problema que é NP-difícil é NP. Um problema que é NPC é NP-difícil e NP ao mesmo tempo (ver Figura 3).

Figura 3: Representação dos problemas NPC em relação aos problemas NP e NP-difíceis

Um problema pode deixar de ser NP-difícil e passar a ser NPC se for encontrada uma redução de um problema NPC para ele.

Se um problema da classe NPC for resolvido, a classe inteira também será, incluindo a classe NP, fazendo com que P=NP. Se for provado que um deles não é resolvível a classe inteira não é resolvível.

O professor contou a história da nomenclatura das classes de complexidade, para que pudéssemos entender melhor como elas foram definidas.

Mais tarde, o professor extrapolou um pouco a matéria e mostrou a hierarquia booleana , onde as classes de problemas (p) são definidas de forma um pouco recursiva. Isso foi feito para mostrar que além da classe de complexidade que estamos estudando existem outras mais complicadas.

6. Um problema NP completo: satisfabilidade de circuitos, CIRCUIT-SAT

6.1. Descrição

Essa sessão apresenta a prova que o problema de satisfabilidade de circuitos é um problema NP-completo. Essa prova usa conceitos básicos de circuitos combinacionais booleanos tais como portas lógicas (AND, OR, NOT), tabelas verdade (onde são armazenadas as operações das portas lógicas) e circuitos combinacionais, que consistem em uma ou mais portas lógicas conectadas por fios. Para definir o problema de satisfabilidade de circuitos, o número de saídas é limitado a 1.

Um circuito combinacional booleano é capaz de satisfação se, a partir de uma dada entrada a saída é 1.

O problema de satisfabilidade de circuitos é: “Dado um circuito combinacional booleano composto de portas AND, OR, NOT, ele é capaz de satisfação?”.

A linguagem formal para esse problema é definida como:

CIRCUIT-SAT = {C: C é um circuito combinacional booleano capaz de satisfação}.

Para provar que este problema é NPC, deve-se provar que ele pertence à classe NP e que ele é NP-difícil.

Para provar que ele pertence à classe NP, basta mostrar que ele é verificável em tempo polinomial, o que é simples.

Para provar que ele é NP-difícil, foi usado um modelo de computação que representa um computador genérico, o que não é trivial de se fazer.

6.2. Discussão em aula

Este tópico foi iniciado com a definição do problema de satisfabilidade por um aluno chamado pelo professor.

A prova que o problema de satisfabilidade de circuitos é um problema NP-completo usa os conceitos de portas lógicas e tabelas verdade. As portas lógicas que são consideradas para a prova são AND, OR e NOT, além disso, para as portas AND e OR é considerado apenas o caso básico de duas entradas e uma saída. As tabelas verdade armazenam as operações das portas lógicas.

O problema de satisfabilidade de circuitos, conhecido como CIRCUIT-SAT, é: “Dado um circuito combinacional booleano composto de portas and, or e not ele é capaz de satisfação?”. Ou seja, existe uma forma de atribuir valores para essa seqüência de entrada de tal forma que a saída seja 1?

Esse problema tem aplicabilidade na área de otimização de hardware auxiliada por computador. Se um subcircuito sempre produz saída 0, ele pode ser substituído por um subcircuito mais simples que omite todas as portas lógicas e fornece o valor constante 0 como saída.

Dependendo da instância do problema, ele pode ser resolvido em tempo polinomial, mas ele não garante que para toda entrada ele vai ser de tempo polinomial. Por exemplo, se o circuito não tiver porta not, só tiver and e or, o problema poderia ser resolvido em tempo polinomial.

A prova de que esse problema pertence à classe NPC é feita em duas etapas. Primeiro deve-se provar que ele está em NP, mostrando que ele é verificável em tempo polinomial. A segunda parte consiste em provar que ele está em NP-dificil, o que é mais complicado porque é necessário argumentar usando um modelo de computação. Nesse caso, foi usado o modelo que representa um computador genérico.

Para provar que um problema é NP-dificil, deve-se mostrar que todo problema NP é redutível a ele. A dificuldade dessa prova está na definição do modelo de computação que será usado.

A partir da prova que o problema de satisfabilidade de circuitos é, ao mesmo tempo, NP e NP-dificil chegou-se ao teorema que diz que “O problema de satisfabilidade de circuitos é NPC”.

7. Redução de CIRCUIT-SAT a SAT

7.1. Descrição

Outra forma de provar que uma linguagem L é NPC é usar um lema que diz: “Se L é uma linguagem tal que L’ L para alguma L’ ∈ NPC, então L é NP-difícil. Além disso, se L ∈ NP, então L ∈ NPC”. Esse lema fornece um método para provar que uma linguagem L ∈ NPC.

1. Prove que L ∈ NP

2. Selecione uma linguagem NPC conhecida L’

3. Descreva um algoritmo de calcule uma função de redução f

4. Prove que a função satisfaz a x ∈ L’ se e somente se f(x) ∈ L para todo x {0,1}^*.

5. Prove que o algoritmo que calcula f é executado em tempo polinomial

Um exemplo desse método é a prova de que SAT é NPC, usando a redução de CIRCUIT-SAT a ele.

O problema de satisfabilidade de fórmulas perguntas se uma dada fórmula boolena é capaz de satisfação. A linguagem formal para este problema é:

SAT={f: f é uma fórmula booleana capaz de satisfação}

Uma fórmula booleana f é composta por n variáveis booleanas, m conectivos booleanos (qualquer função booleana que tenha 1 ou 2 entradas e 1 saída) e parênteses.

Para provar que SAT ∈ NPC, primeiro deve-se provar que ele pertence a NP, mostrando que ele é verificável em tempo polinomial e depois que ele é NP-difícil mostrando que CIRCUIT-SAT SAT.

Para provar que CIRCUIT-SAT SAT, basta mostrar que qualquer instância de satisfabilidade de circuito pode ser reduzida em tempo polinomial a uma instância de satisfabilidade de fórmula.

7.2. Discussão em aula

Esse tópico foi iniciado com o aluno definindo o problema SAT.

SAT é uma linguagem que formaliza o problema de satisfabilidade de fórmulas. Esse problema pergunta se uma dada fórmula booleana é capaz de satisfação. Uma instância de SAT é uma fórmula booleana composta de n variáveis booleanas, m conectivos booleanos e parênteses.

Para fazer a redução de CIRCUIT-SAT a SAT, deve-se transformar o circuito em uma fórmula booleana. O que deve ser feito em tempo polinomial.

Para provar que SAT é NPC, foi provado que ele é verificável em tempo polinomial e que CIRCUIT-SAT pôde ser reduzido a ele em tempo polinomial.

A diferença entre SAT e CIRCUIT-SAT, é que SAT é um problema de satisfabilidade de fórmulas e CIRCUIT-SAT é um problema de satisfabilidade de circuitos.

8. Conclusão

Essa aula gerou muitas dúvidas, pois se trata de um tópico muito complexo. A cada item perguntado pelo professor, as dúvidas que surgiram foram prontamente esclarecidas por ele usando exemplos e às vezes contando um pouco da história da complexidade de algoritmos.

Algumas conclusões tiradas durante o decorrer da aula foram:

· A linha de pesquisa de complexidade de algoritmos desenvolveu caminhos bastante complicados.

· Está faltando um bom trabalho sobre modelos de computação pra simplificar as provas. É complicado trabalhar direto com modelos de computação.

E, por fim, uma curiosidade sobre a prova de problemas NPC: O 1º problema a ser provado como um problema NPC foi o SAT. Sua prova foi feita usando a comparação direta com a máquina de Turing que é um dos modelos de computação existentes. Outros exemplos de modelos de computação são algoritmos de Markov e funções recursivas.