Universidade Estadual de Campinas
Instituto de Computação
MO640 – Biologia Computacional Prof. Dr. João Meidanis
Discente: Pedro Henrique Del Bianco Hokama RA:063658
Ata de aula – 26/08/2008 - Sobre a aula de 21/08/2008
1. Crie uma planilha eletrônica que construa a matriz necessária para calcular a similaridade local entre duas seqüências S e T.
Veja a planilha em anexo:
Planilha Eletrônica (.ods)
Planilha Eletrônica (.xls)
2. Calcule a similaridade local entre as seqüências: AGTCGTGAC e CGTAGTCCGTGAT. Use pontuação match=1, mismatch=0, gap=-2. Faça primeiro na mão e depois confira com a sua planilha.
A similaridade local obtida pelo calculo manual dos alunos foi 6, o mesmo obtido pela planilha eletrônica, veja a figura abaixo

3. Crie uma planilha eletrônica que construa a matriz necessária para calcular a similaridade semi-global entre duas seqüências S e T.
Veja a planilha em anexo:
Planilha Eletrônica (.ods)
Planilha Eletrônica (.xls)
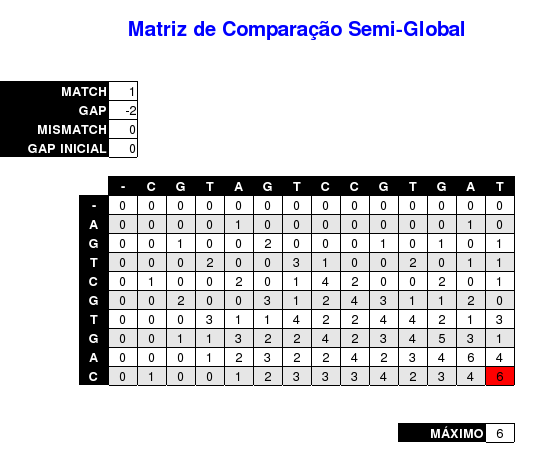
4. Calcule a similaridade semi-global, sem cobrar por espaços nas extremidades, entre as seqüências: AGTCGTGAC e CGTAGTCCGTGAT. Use pontuação match=1, mismatch=0, gap=-2. Faça primeiro na mão e depois confira com a sua planilha.
A similaridade semi-global obtida pelo cálculo manual foi 6, o mesmo obtido pela planilha eletrônica, veja a figura abaixo
5. Notamos que as similaridades entre as seqüências AGTCGTGAC e CGTAGTCCGTGAT obedecem: global ≤ pontas livres ≤ local. Isto vai se verificar para todo par de seqüências? Por que?
A afirmação de que a similaridade global ≤ pontas livres ≤ local
é verdadeira, mas apenas com a condição de que gap ≤ 0.
Prova:
Sejam sim-gbl(S,T), sim-sgbl(S,T) e sim-lcl(S,T), o valor da similaridade global, semi-global e local, respectivamente, entre duas seqüências S e T.
Estas similaridades correspondem a pontuações de alinhamerntos
ótimos. Para determinar as similaridades global e semi-global,
usamos alinhamentos que cobrem as seqüências em sua totalidade,
tanto S como T. O que difere é a maneira de pontuar. Existe a
pontuação global, pont-gbl, e existem várias versões semi-globais,
que não cobram por espaços em algumas das extremidades. Aqui
consideraremos a pontuação que não cobra por espaços em nenhuma
extremidade, que chamaremos de pont-sgbl, mas o mesmo raciocínio
se aplica a todas as outras versões.
Alinhamentos locais são diferentes. Eles não necessariamente envolvem
as seqüências inteiras, ao contrário dos alinhamentos globais e
semi-globais, mas restringem-se a trechos contínuos das seqüências
comparadas. A maneira de pontuar alinhamentos é a mesma usada
para os alinhamentos globais, ou seja, pont-gbl.
Sejam A, A' e A'' respectivamente alinhamentos ótimos global,
semi-global e local. Temos que:
sim-gbl(S,T) = pont-gbl(A),
Os alinhamentos A e A' são do mesmo tipo, ou seja, envolvendo as
seqüências inteiras, portanto podemos pontuá-los com pont-gbl ou
com pont-sgbl, e sabemos que:
sim-sgbl(S,T) = pont-sgbl(A'),
sim-loc(S,T) = pont-gbl(A'').
pont-sgbl(A) ≤ pont-sgbl(A'), e
pois A e A' são ótimos para as respectivas pontuações. Porém, também
podemos dizer que, em virtude de gaps serem sempre pontuados
com valores negativos ou nulos, para qualquer alinhamento B
vale:
pont-gbl(A') ≤ pont-gbl(A),
pont-gbl(B) ≤ pont-sgbl(B).
uma vez que pont-sgbl não penaliza por espaços nas pontas.
Juntando algumas das observações acima, temos:
sim-gbl(S,T) = pont-gbl(A) ≤ pont-sgbl(A) ≤ pont-sgbl(A') = sim-sgbl(S,T).
Fica assim provada a parte "global ≤ pontas livres" da afirmação. Vamos provar agora a parte "pontas livres ≤ local".
Observe que se retiramos as
extremidades não pontuadas de A', ficamos com um alinhamento local
A''' que satisfaz:
pont-sgbl(A') = pont-gbl(A''').
Sendo assim, temos:
sim-sgbl(S,T) = pont-sgbl(A') = pont-gbl(A''') ≤ pont-gbl(A'') = sim-lcl(S,T).
Note que nesta parte não precisamos supor nada sobre a pontuação de gaps. Com isso concluimos a prova.