[Previous chapter] [Next chapter]

Building stochastic models


In this chapter we look in detail at how users can build stochastic models in Xpress-SP using the functionalities available in the mmsp module. The steps and issues related to scenario generation, model formulation, and solution analysis are addressed here. Although the framework for building stochastic models is flexible, users are advised to follow the model-building procedures in a sequential fashion as shown below.

Setting stages

Stages are set using the function spsetstages(Stages: set); e.g., 

 declarations
  T=4
  Stages=1..T
 end-declarations
 spsetstages(Stages)

The set Stages can be of type integer or string, or it can be a range.

SPrands and SPrandexps

Each sprand corresponds to a stochastic event (Maths/xi.pngt), and hence its stage and possible values must be set by the user. sprandexps on the other hand are expressions built using sprand, and therefore their stages and values are automatically defined.

Declaring and associating sprand with stages

Random variables are declared as sprand in mmsp. 

 declarations
  demand, price :array(2..T) of sprand
 end-declarations

It is recommended that at the time of declaration of arrays of sprand, all the sets used for indexing such arrays be constant or finalized (i.e. elements of sets are known and sizes of sets are fixed). At the time of declaration, sprand are automatically `created', however if one or more of the sets used for indexing an array of sprand are dynamic then by default such an array is dynamic in nature. In this case, users will have to explicitly create all the sprand using the create procedure (e.g., T:=4; forall(t in 2..T) create(demand(t)).

Users can set the stage of sprand using the function spsetstage(srnd: sprand). One or more sprand in each stage may correspond to the Maths/xi.pngt for that stage; e.g., 

 forall(t in 2..T)  spsetstage(demand(t),t)
 forall(t in 2..T)  spsetstage(price(t),t)

In the above example, the pair (demandt, pricet) corresponds to the random event Maths/xi.pngt. Note that users may not have to set the stages of all sprand if the parameter xsp_implict_stage is set to true (see Section Setting SP parameters). Also note that one could dissociate an sprand from a stage by setting its stage to XSP_STAGE_ZERO.

Operators

The operators: +, -, *, /, and ^ can be used with types real, sprand, and sprandexp to create new spradexp, e.g., 

 declarations
  tot_demand: sprandexp
 end-declarations
 tot_demand:=sum(t in 2..T) demand(t)

Relational conditions

Relational conditions, which themselves are of type sprandexp, can be created using the relational operators: <=, >=, and =, together with real, sprand, and sprandexp.

Logical conditions

Logical conditions, which in turn are of type sprandexp themselves, can be created using relational conditions together with `and', `or', `not' or a combination of these, e.g., 

declarations
  if_demand_demand: sprandexp
 end-declarations
 if_pos_demand:= (demand(2)+demand(3))>=demand(1) or 
                  demand(1)>=0

Functions

The general format of all the functions involving sprand and sprandexp is: f(args):sre where f is the name of the function, args are the arguments of this functions, and sre is a sprandexp. This is further described in the following section.

One argument

f: abs, ceil, floor, round, ln, exp
arg1: sprand or sprandexp

Two arguments

f: maximum, minimum
arg1, arg2: real, sprand, or sprandexp

Three arguments

f: spif
arg1: sprandexp (must be a logical or relational condition)
arg2, arg3: real, sprand, or sprandexp (arg2, arg3 correspond to true and false values of the condition)

e.g., if sr1, sr2, and sr3 are sprand then following is a valid usage of spif:
sre:=spif(sr1<=3 and sr1>=sr2^sr3, 1, maximum(sr2,ceil(sr1))) Here whenever arg1 evaluates to true, sre is assigned arg2 otherwise it is assigned arg3.

Scenario tree

Generation

The first step in building a stochastic model is the creation of the scenario tree (see e.g. Section Scenario generation).

SP/m4d5d8348.png

Figure 5.1: Multi-stage scenario tree

where,
T = Number of stages
S = Number of Scenarios
Nt = Number of nodes in stage t (N1=1, NT=S)
Ps = Probability of scenario s, such that Maths/sumsm.pngSs=1 Ps = 1
Maths/xi.pngt,nt = Assumed value of random variable Maths/xi.pngt at node (t,nt)
Pt,nt = Conditional probability of occurrence of event Maths/xi.pngt,nt (at node (t,nt))

Creation of a scenario tree involves setting of its stages followed by declaration and association of each sprand with a stage.

Exhaustive tree

All independently distributed sprand

If all the random variables in the model are independent, then one can first specify their discretized distribution and generate the tree as follows: 

 declarations
  nElem=3 
  Elems = 1..nElem
  demand:array(2..T) of sprand
  value,probability:array(2..T,Elems) of real 
  val,prob:array(Elems) of real
 end-declarations
 
 value:=[5,10,0,  
         7,12,13,  
         12,14,0]
 probability:=[.5,.5,0,  
               .2,.6,.2,  
               .6,.4,0] 
 
 forall(t in 2..T) do
  forall(e in Elems) prob(e):=0
  forall(e in Elems) prob(e):=probability(t,e)
  forall(e in Elems) val(e):=value(t,e)
  spsetdist(demand(t),val,prob)
 end-do
 spgenexhtree

This will create a tree with 2 branches from first stage nodes, 3 branches from second stage nodes, and 2 branches from third stage nodes, implying a total of 2 · 3 · 2 = 12 scenarios.

SP/m535e63a.png

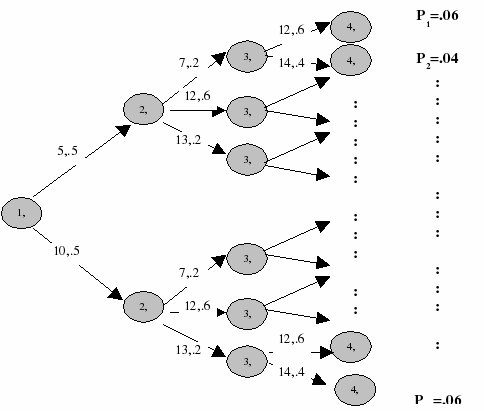
Figure 5.2: Exhaustive scenario tree

Note that in the exhaustive generation, the size of the scenario tree increases rapidly with an increase in the number of sprand. If in the above-mentioned example, we add another random variable pricet, with price2, price3, and price4 assuming 3, 2, and 2 discrete values in the second, third, and fourth stage respectively, then the number of scenarios would be (2 · 3) · (3 · 2) · (2 · 2) = 144.

Some jointly distributed sprand

One can also create a scenario tree with some or all sprand jointly distributed. The following example demonstrates how to build a 3-stage scenario tree, with three sprand namely sr1, sr2 and sr3, where sr1 and sr2 belong to the second stage and sr3 belongs to the third stage. It is assumed that sr1 and sr3 are jointly distributed, whereas sr2 is independently distributed. 

 declarations
  T=3
  Stage=1..T
  sr1,sr2,sr3: sprand 
 end-declarations

 ! set stages
 spsetstages(Stage)
 spsetstage(sr1,2)
 spsetstage(sr2,2)
 spsetstage(sr3,3)
 
 ! set independent distribution of sr2 = {10 w.p .2, 20 w.p .8}
 declarations
  ind_val,ind_prob:array(1..2) of real 
 end-declarations

 ind_val:=[10,20]
 ind_prob:=[.2,.8]
 spsetdist(sr2,ind_val,ind_prob)
 
 ! set joint distribution of sr1 and sr3 {(25,45) w.p .3, (35,55)
 w.p .7}
 declarations
  joint_val:array(1..2,1..2) of real
  joint_prob:array(1..2) of real
  SetSrnd:set of sprand 
 end-declarations
 
 joint_val:=[25,35, 45,55]
 joint_prob:=[.3,.7]
 SetSrnd:={sr1,sr3}
 spsetdist(SetSrnd,joint_val,joint_prob)

 ! generate exhaustive tre
 spgenexhtree

The following exhaustive tree is created:

SP/m6b2a4d41.png

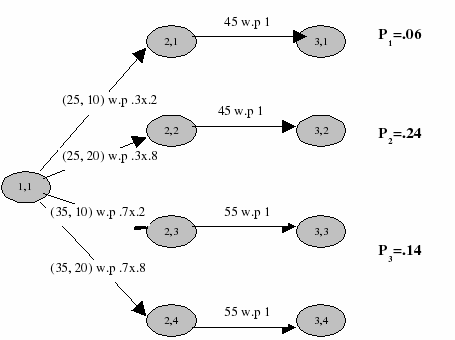
Figure 5.3: Exhaustive scenario tree with some jointly distributed random variables

Stage symmetric

Creating trees

Users may also want to create symmetric trees, e.g., a tree with three branches from each node in each stage. This can be done using the function 

 spcreatetree(3)

Users must specify the realized values and the conditional or the scenario probabilities afterwards. Similarly, a tree with two branches from the first stage node, 3 branches from each node in the second stage, and 2 branches from each node in the third stage, can be generated as follows: 

 declarations
  branches:array(2..T) of integer 
 end-declarations
 branches:=[2,3,2]
 spcreatetree(branches)

Specifying values of sprand and conditional probabilities

Once a tree is created explicitly, the default value of all sprand in the scenario tree is zero. mmsp provides functions for setting the assumed value of sprand in the scenario tree based on the tree's structure. If the tree is symmetric with respect to stage (or is symmetric across all the stages), then it can be accomplished as follows: 

! Assume branches:=[2,3,2] is already set
 declarations
  MaxBranch=3
  Branches=1..MaxBranch
  value:array(2..T,Branches) of real
  Val:array(Branches) of real
  probability:array(2..T,Branches) of real
  prob:array(Branches) of real
 end-declarations

 value:=[5,10,0,
         7,12,13,
        12,14,0]
 forall(t in 2..T) do
  forall(b in Branches) Val(b):=value(t,b)
  spsetrand(demand(t),Val)
 end-do
 probability:=[.5,.5,0,
               .2,.6,.2,
               .6,.4,0] 
 forall(t in 2..T) do
  forall(b in Branches) prob(b):=probability(t,b)
  spsetcondprob(t,prob)
 end-do

This will generate a scenario tree as shown in Figure Exhaustive scenario tree.

Explicit tree

Users may also create a tree (usually asymmetrical) using the following functionalities in mmsp:

Creating a tree

Assume T=3, and user wants to create the following tree

SP/4c23ea46.png

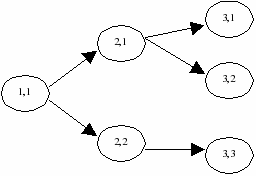
Figure 5.4: Explicit scenario tree - node numbers

Creating a tree with trap stages

A tree with a trap stage consists of at least one path that does not necessarily end at the last stage. An example of such a tree is shown in the following figure:

SP/mb301883.png

Figure 5.5: Explicit scenario tree - node numbers

Such a tree can also be built using the function spcreatetree(NodeNum) as shown earlier where, 

 S=4;
 NodeNum:=[1,1,1,
           1,1,2,
           1,2,0,
           1,3,3];

Note that the stochastic problem associated with such a tree cannot be scenario based, since all scenarios don't exist, therefore xsp_scen_based must be set to false.

Setting realized sprand and probabilities

An sprand can be set using the function spsetrandatnode, e.g., 

 declarations
  N:array(1..T) of integer     ! Total number of nodes in each stage
  value:array(2..T,1..S) of real
  probability: array(2..T,1..S) of real
 end-declarations
 N:=[1,2,3]
 value:=[5,10,0,  
         7,12,13]
 forall(t in 2..T,n in 1..N(t)) spsetrandatnode (demand(t),n,value(t,n))
 probability:=[.5,.5,0,
               .2,.8,1]
 forall(t in 2..T,n in 1..N(t)) spsetprobcondatnode (t,n, probability(t,n))

The scenario tree thus created would look as follows:

SP/m1eb08d52.png

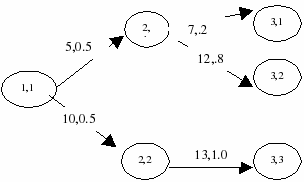
Figure 5.6: Explicit scenario tree - values and probabilities

For the scenario-based problems, users may set the scenario probabilities explicitly using the function spsetprobscen(scen_num: integer, prob: real).

Manipulation

Xpress-SP supports a few scenario manipulation routines such as aggregation and deletion of scenarios. Scenario manipulation can also be done interactively in Xpress-IVE (see Section Analyzing in IVE).

Aggregating all scenarios emerging from a common ancestral node

All the scenarios emerging from an ancestral node in a scenario tree can be aggregated to create one aggregated scenario. Consider following scenario tree:

SP/718673c2.png

Figure 5.7: Original scenario tree

Here, scenarios 1 to 3 can be aggregated as follows:

 spaggregate(1..3)

Note that the new scenario tree is renumbered as follows:

SP/m74d5ad04.png

Figure 5.8: Aggregated scenario tree - scenarios 1 to 3

Hence, in order to aggregate scenarios 1 to 3 and scenarios 4 to 5 shown in Figure Original tree separately, the function call should be made in the following order: 

 spaggregate(4..5)
 spaggregate(1..3)

This will result in the following tree:

SP/m394bb4c.png

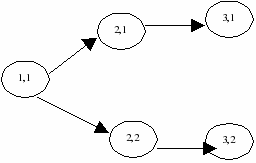
Figure 5.9: Aggregated scenario tree - scenarios 1 to 3 and 4 to 5

Similarly, scenarios 1 to 5 can be aggregated to create a one-scenario scenario tree.

Aggregated probabilities

SP/1ba83610.png

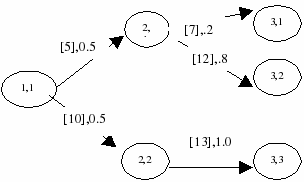
Figure 5.10: Original tree

If scenarios 1 to 2 were aggregated in the above shown tree, the new tree with aggregated values and probabilities would look as follows:

SP/m40db8fc5.png

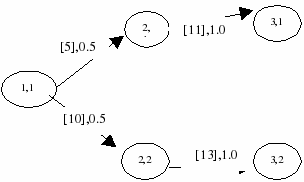
Figure 5.11: Aggregated values

Here, 7 · .2 + 12 · .8 = 11 with probability 1.0. The probability of the aggregated scenarios is the sum of probabilities of the scenarios aggregated.

Aggregating selected scenarios emerging from a common ancestral node

One may also aggregate a set of scenarios (not necessarily contiguous), if none of the nodes after the common ancestral node of the selected scenarios in the path pertaining to the selected scenarios have any siblings. This is illustrated in the following example:

SP/m4318c2fe.png

Figure 5.12: 4-stage scenario tree

In the scenario tree shown above, scenarios 1 and 5 can be aggregated since the node(3,1), node(3,3), node(4,1), and node(4,5) lying after the common ancestral node(2,1) do not have any siblings. The corresponding function call in mmsp would be spaggregate({1,5}).

On aggregation, the nodes corresponding to the selected scenarios are deleted. The new aggregated branch corresponding to the aggregated scenario is appended as the last child of the common ancestral node, and the tree node numbers are updated suitably. The aggregated scenario tree in the above example would look as follows:

SP/m379636f3.png

Figure 5.13: Aggregated tree

Deletion in scenario based problems

Users can delete a scenario using the function spdelscen(s:integer). In this case, the probabilities of the remaining scenarios are re-normalized (i.e., each remaining scenario's probability is divided by one minus probability of deleted scenario). Similarly a set of scenarios can be deleted using the function spdelscen(delSet :set of integer). Again, the probabilities are re-normalized (i.e., each remaining scenario's probability is divided by one minus the sum of probability of deleted scenarios), and based on the updated scenario probabilities, the conditional probabilities are re-normalized. The sprand remain unchanged, whereas the node numbers are updated suitably. This is illustrated pictorially in the following example.

SP/1824ff2c.png

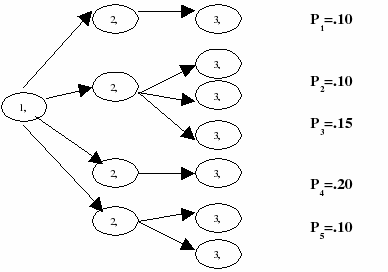
Figure 5.14: 3-stage scenario tree - scenario based

If scenarios 3 and 5 are deleted using the function spdelscen({3,5}), the resulting scenario tree would look as follows:

SP/m6dac8f7f.png

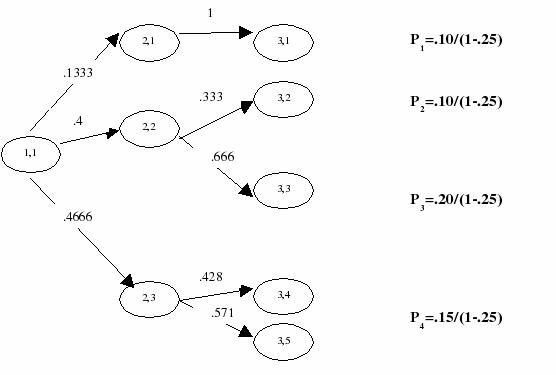
Figure 5.15: Pruned 3-stage tree - scenario based

Deletion in node based problems

Deletion in node-based problems is similar to the one in scenario-based problems, with the exception that the re-normalization of the probabilities is done based on the conditional probabilities of the nodes associated with the deleted scenarios. The following example demonstrates deletion of set of scenarios in a node based problem:

SP/m3abd8c9f.png

Figure 5.16: 3-stage scenario tree - node based

If scenarios 3 and 5 are deleted using spdelscen({3,5}), then the resulting scenario tree looks as follows:

SP/b18991e.png

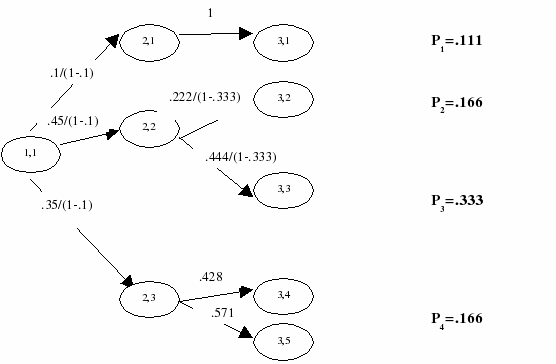
Figure 5.17: Pruned 3-stage tree - node based

Traversing

Users may use several scenario tree related functions such as:

Evaluating

One can evaluate the realized value of sprands and sprandexps in the scenario tree using the function speval(sptype,scen):real or speval(sptype,stage,node):real e.g., if sr1 and sr2 are of type sprand, and sre is an sprandexp, then the value of sre:=sr1+sr2 at the fourth node in the third stage can be evaluated by calling the function speval(sre,3,4). Calling speval(sre) would return the expected value of sre.

Debugging

One can print the scenario tree loaded in Xpress-SP by calling the function spprinttree.

Formulation

Formulating a stochastic problem in the Xpress-SP syntax involves declarations of spvar and splinctr. The model formulation is discussed below.

Stochastic variables and constraints

Each stochastic variable must be associated with a stage. The stage of a constraint is automatically defined by the stages of the variables and other stochastic entities used to build the constraint.

Declaring and associating spvar with stages

The spvar are declared as follows: 

 declarations
  x:array(1..T) of spvar
 end-declarations

It is recommended that at the time of declaration of arrays of spvar, all the sets used for indexing such arrays are `finalized' (i.e. elements of sets are known and sizes of sets are fixed). At the time of declaration, spvar are automatically `created', however if one or more of the sets used for indexing an array of spvars are not `finalized' (e.g. in the above example, if the value of T is not known at the time of declaration), then by default such an array is `dynamic' in nature. In this case, users will have to explicitly `create' all the spvar using the procedure create (e.g., T:=4; forall(t in 1..T) create(x(t))).

Spvars may be associated with a stage (unless xsp_implict_stage is set to true (see Section Setting SP parameters)) e.g.

 forall(t in 1..T) spsetstage(x(t),t)

One could also disassociate a spvar from a stage by setting its stage to XSP_STAGE_ZERO.

Setting types and bounds

The type of decision variables can be set using the is_integer, is_binary, and is_free attributes. The bounds can be set by using unnamed unary constraints, e.g., if x is of type spvar and srn is of type sprandexp, then the constraint x<=srn sets the upper-bound of x. Of course, the bounds can be real, sprand or sprandexp.

Writing the objective function and constraints

The objective function and constraints (type splinctr) may be declared as follows: 

 declarations
  Obj, Ctr:splinctr
 end-declarations

The following points must be kept in mind while a writing model in Xpress-SP:

Manipulation

spvar may be fixed at a certain value using the function spfix(x: spvar, val: real). spunfix can be used on spvar to unfix them. Similarly, splinctr may be hidden or unhidden using the function spsethidden(c: splinctr, cond: boolean). If the second is true, then the constraint is hidden, else it is unhidden. Note that if all the variables of a constraint are fixed, then the constraint is automatically hidden. These functionalities are particularly useful if the user wants to fix some variables e.g., the entire first stage variables at a pre-determined value and solve the problem in the recoursed stochastic framework (see Section Solution measures).

Stochastic problem

The stochastic problem is automatically generated when optimization routine (maximize or minimize) is called. The type of the matrix generated depends on whether the problem is node based or scenario based. Additionally, related problems may also be generated by passing suitable options to the optimization routine.

Setting Xpress optimizer control variables

Users may set the optimizer control parameters using the function setparam e.g., setparam('xprs_presolve',0) will turn the presolve off. All the controls related to the optimizer are listed in the mmsp module.

Optimizing

The problem can be optimized by calling the procedures maximize(Obj: splinctr) or minimize(Obj: splinctr). At this point, the validity of the scenario tree is checked. If no tree exists then an exhaustive tree is attempted to be built (by calling the function spgenexh internally). The problem is then internally expanded and sent to the optimizer. The optimizer control parameters for this problem are also set.

Instance of problem in a scenario

Instead of optimizing the fully expanded problem, once could optimize an instance of a problem in a particular scenario s (see Section Focus on an instance of the problem) by calling maximize(Obj: splinctr, s: integer) or maximize(Obj: splinctr, s: integer). Note that the parameter xsp_scen_based should be set to true.

Instance of problem at a node in the scenario tree

Similarly one could optimize an instance of a problem at a particular node(t,n) (see Section Focus on an instance of the problem) in a scenario tree by calling maximize(Obj: splinctr, t: integer, n: integer) or maximize(Obj: splinctr, t: integer, n: integer). Note that the parameter xsp_scen_based should be set to false.

Options

Users may also pass an option string to indicate the algorithm and type of problem to be solved by calling the function maximize(Obj: splinctr, option: string) or minimize(Obj: splinctr, option: string). The options and their meanings are listed below:

As an example, if the user wants to maximize `Profit' — an splinctr — by solving only the LP relaxation of a 4-stage mixed integer problem in a recoursed expected value framework by fixing first stage variables at their expected values and hiding the first stage constraints, using Xpress' barrier routine, the corresponding function call would be: 

 maximize(Profit, XSP_OPT_LP_ONLY+XSP_BARRIER+XSP_EV+XSP_REC)

Exporting problems

Using the optimization routines spexportprob, maximize or minimize and the constants defined in Xpress-SP one could also export problems. The spexportprob procedure is overloaded as follows:

where argument,

  1. dir can be XSP_MAX or XSP_MIN
  2. objfn is the objective function of type splinctr
  3. filetype can be XSP_X_LP, or XSP_X_SP, or XSP_X_SMPS, or XSP_X_SMPS_FREE
  4. filename is the name of the file in which the exported problem will be stored.

SP file

For the purpose of debugging the underlying SP model, one could export the problem .sp file. For instance, spexportprob(XSP_MIN, Obj, XSP_X_SP, 'myfile') will export the problem in the file myfileProb.sp, whereas minimize(Obj, XSP_X_SP) will both export the stochastic problem in the file ObjProb.sp as well as minimize the problem.

SMPS files

The time, core, and scenario files pertaining to stochastic problem can be exported .e.g., in the free format by calling exportprob(XSP_MAX, obj, XSP_X_SMPS_FREE). This will create the files objSMSP.tim, objSMSP.sto, and objSMPS.cor. Alternatively user may create these files and optimize the problem by calling maximize(obj, XSP_X_SMSP_FREE). Note that if the constant XSP_X_SMSP is used then files are exported in the fixed format.

LP problem

The problem currently loaded in the optimizer can be exported in an lp file by calling spexportprob(XSP_MAX, obj, XSP_X_LP) or maximize(obj, XSP_X_LP).

Getting attributes of a problem from the optimizer

If problem is solved using Xpress optimizer, users may get the status of the problem after optimization by obtaining various integer, real, and string attributes using the function getparam. It is advised that the user checks the optimization status, e.g., xprs_lpstatus and/or xprs_mipstatus, before getting the values of the objective function and other related solutions, comparing the values of these attributes with the constants — XSP_LP_OPTIMAL, XSP_LP_INFEAS, XSP_LP_CUTOFF, XSP_LP_UNFINISHED, XSP_LP_UNBOUNDED, XSP_LP_CUTOFF_IN_DUAL, XSP_MIP_NOT_LOADED, XSP_MIP_LP_NOT_OPTIMAL, XSP_MIP_LP_OPTIMAL, XSP_MIP_NO_SOL_FOUND, XSP_MIP_SOLUTION, XSP_MIP_INFEAS, or XSP_MIP_OPTIMAL.

Getting solution

If the problem is feasible then users can obtain the solution value and reduced cost of spvar, and the activity or slack value of splinctr in a scenario or at a node in the scenario tree. The values of the first stage entities can be found using the following functions: 

 getsol(svar: spvar):real
 getrcost(svar: spvar):real
 getslack(sctr: splinctr):real
 getdual(sctr: splinctr):real

These functions may also be used for spvar or splinctr belonging to any stage in an Expected value (see Sections Expected Value problem with recourse) or a focused (see Sections Focus on an instance of the problem) problem.

Solution in a scenario

For fully expanded problems, the values of entities can also be obtained in a particular scenario, e.g., 

 getsolinscen(svar: spvar, scen: integer):real
 getrcostinscen(svar: spvar, scen: integer):real
 getdualinscen(sctr: splinctr, scen: integer):real
 getslackinscen(sctr: splinctr, scen: integer):real

Solution at a node in the scenario tree

Similarly, the solution can also be obtained at a particular node:

 getsolatnode(svar: spvar, node: integer):real
 getrcostatnode(svar: spvar, node: integer):real
 getdualatnode(sctr: splinctr, node: integer):real
 getslackatnode(sctr: splinctr, node: integer):real

Note: if svar or sctr belongs to stage t, then node must belong to {1,...,Nt}.

Evaluation

One can evaluate the solution or fixed value of spvar or realized value of and splinctr in the scenario tree using the function speval. The function syntax is similar to the one shown in Section Deletion.

Other functions

Users may also override the names of spvar, splinctr, and sprand that are displayed in IVE, by setting their names using the procedure spsetname.

Debugging

Writing the problem loaded in the optimizer memory

The fully expanded problem is loaded in the optimizer only at the point when optimization is called; hence, a problem can be exported only after optimization is complete. The function for exporting the problem is spwriteprob(filename: string, flags: string). It replicates the function XPRSwriteprob provided in the Xpress optimizer library. Please refer to the optimizer reference manual for description on the parameters `filename' and `flags'.

Setting SP parameters

The following control parameters are available in Xpress-SP suite:

XSP_IVE_ENABLE
This parameter when set to false, disables IVE access to entities in stochastic model.
Default: true.
XSP_TOLPROB_LB, XSP_TOLPROB_UB
These are the tolerances on the probabilities (e.g., distribution, conditional, and scenario probabilities). Specifically, if p is one of these probabilities, then XSP_TOLPROB_LB Maths/leq.png p Maths/leq.png 1 + XSP_TOLPROB_UB.
Default: 10-6, 10-6 respectively.
XSP_TOLPROB_TOTLB, XSP_TOLPROB_TOTUB
These are the tolerances on the total probabilities that should sum to 1 (e.g., distribution, conditional, and scenario probabilities). If Maths/sumsm.pngp is one these probabilities, then 1 - XSP_TOLPROB_TOTLB Maths/leq.png Maths/sumsm.pngp Maths/leq.png 1 + XSP_TOLPROB_TOTUB.
Default: 0.05, 0.05 respectively.
XSP_SCEN_BASED
If this is set to true, then the model will be expanded based on scenarios instead of nodes.
Default: 0
XSP_COND_PROB
If it is set to false, the conditional probabilities may not sum to 1, and product of the conditional probabilities in a scenario may not be equal to scenario probability. However, if XSP_SCEN_BASED is false, then XSP_COND_PROB is automatically set to true.
Default: true.
XSP_SCALE_PROBS
If set to false, the probabilities will not be scaled to sum to 1.
Default: true.
XSP_LOADNAMES
If set to false, the names of stochastic entities will not be loaded into matrix.
Default: true.
XSP_IMPLICIT_STAGE
Users may not have to set the stages of the sprand and spvar if this parameter is set to true. If the sprand or spvar are grouped in arrays, then they are automatically associated with the stages assuming that the last indexing set is the stage set. If any of the sprand or spvar is not stored in arrays, then it is associated with the first stage. Users may override the automatic association (when XSP_IMPLICIT_STAGE is true) of sprand or spvar with stages by explicitly setting their stage.
Default: false.
XSP_VERBOSE
If it is set to false then IVE will disable the optimizer messages that are displayed in the output text window.
Default: true.
XSP_DISP_WARNINGS
If it is set to false then warnings will not be displayed. Default: true.
XSP_RE_INIT
May be set to false when solving structurally similar problems sequentially, e.g., problem instances in different scenarios (see Section Focus on an instance of the problem).
Default: true.
XSP_CREATE_TREE
If set to false it prevents creation of nodes in the scenario tree. Helpful, if creation of an exhaustive tree based on distributions is not required. (Note: if xsp_create_tree is set to false then XSP_IVE_ENABLE must be set to false)
Default: true.

Chance constraints

Users may model chance constraints in Xpress-SP by using the global constraints functionality. A regular stochastic constraint, say of the form: Maths/sumsm.png
t'
t=1
xt Maths/approx.png b˜t' for some t' is expanded internally as Maths/sumsm.png
(t',n')
(t,n):Node(t,n) Maths/insm.png Path to Node(t',n')
xt,n Maths/leq.png b (t',n') in a node-based problem, i.e., constraints are replicated for all nodes in stage t', or as Maths/sumsm.png
t'
t=1
xts Maths/approx.png bt's Maths/forall.pngs Maths/in.png {1,...,S} in a scenario based problem i.e., constraints are replicated for all scenarios. By setting such as constraint as of type `global', it may be expanded as Maths/sumsm.png
t'
t=1
Maths/sumsm.png
Nt
n=1
Ptnxtn Maths/approx.png Maths/sumsm.png
Nt'
n'=1
Pt'n'bt'n' in a node-based problem, i.e., the constraint is summed across all nodes in stage t' weighted by probabilities of nodes. Similarly, in a scenario-based problem the constraint will be expanded as Maths/sumsm.png
S
s=1
Psxts Maths/approx.png Maths/sumsm.png
S
s=1
Psbt's , i.e., the constraint is summed across all nodes in stage t' weighted by probabilities of scenarios.

Hence, one may model a chance constraint, for instance in a scenario-based problem, by introducing a binary variable z, and setting a constraint C:=Z<=beta of type global by calling spsettype(C, XSP_GLOBAL). Consequently, the constraint will be expanded internally as Maths/sumsm.png
S
s=1
Pszs Maths/leq.png Maths/beta.png , resulting in restricting the total probability of scenarios where z can be one to Maths/beta.png.

Analyzing in IVE

The Xpress Integrated Visual Environment (IVE) provides tools for analyzing the matrix structure, scenarios, and the solution values and distributions of various entities in the model across all the scenarios (see Figure IVE SP interface).

SP/m771f79f9.png

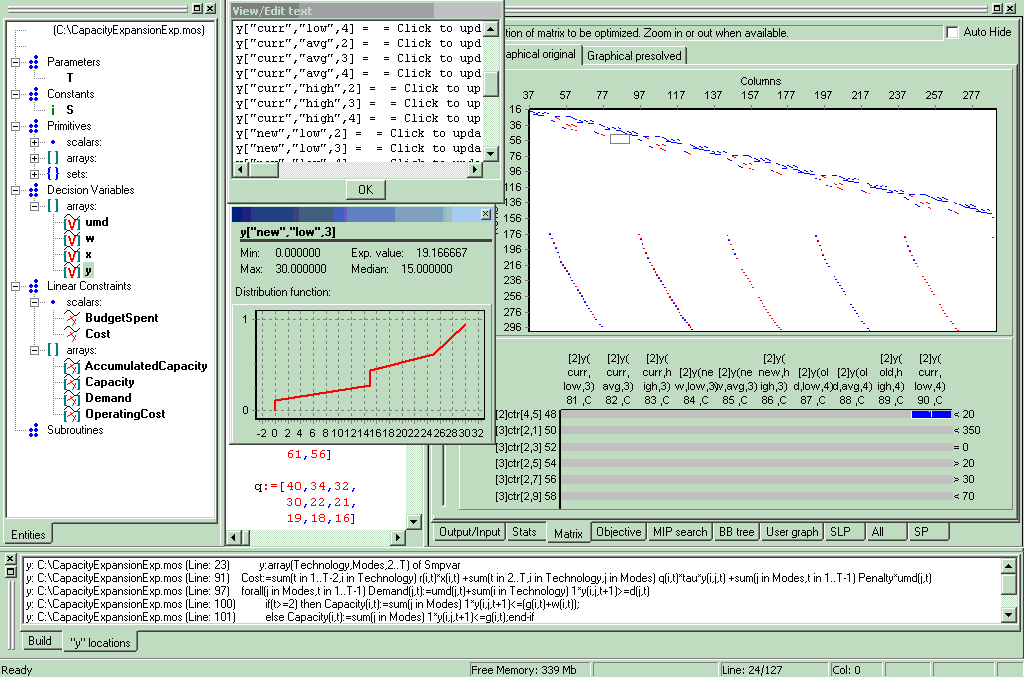
Figure 5.18: IVE SP interface

IVE provides additional features like SP scenario form, Stochastic Dashboard, and Matrix View for visualizing, manipulating, and analyzing stochastic problems.

SP scenario form

The SP form provides list, pie, and block views of the generated scenario tree.

SP/m7d104009.png

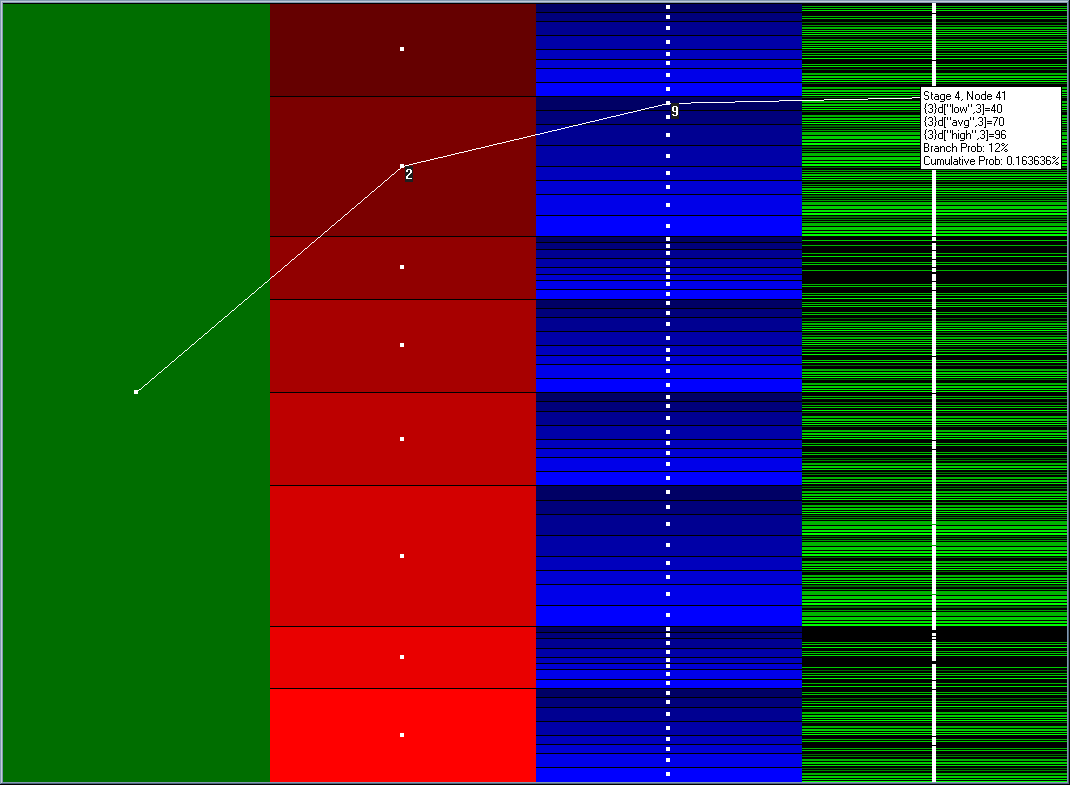
Figure 5.19: Scenario tree block view

Stochastic dashboard

The dashboard provides the model information, namely, the number of stages, spvar, sprand, splinctr, and scenarios. The dashboard also lists the sprand, spvar, splinctr, and scenario indices in the model. Each of these is prefixed by its stage number in curly brackets. The dashboard also gives a miniature version of the scenario tree in the block and the pie view. Users may click on any entity (sprand, spvar, or splinctr) to see its cumulative probability distribution (with statistics like min, max, median and expected values) across scenarios. Users may also select one or more scenarios with any entity to see its values in those scenarios (see fig below).

SP/7479fa11.png

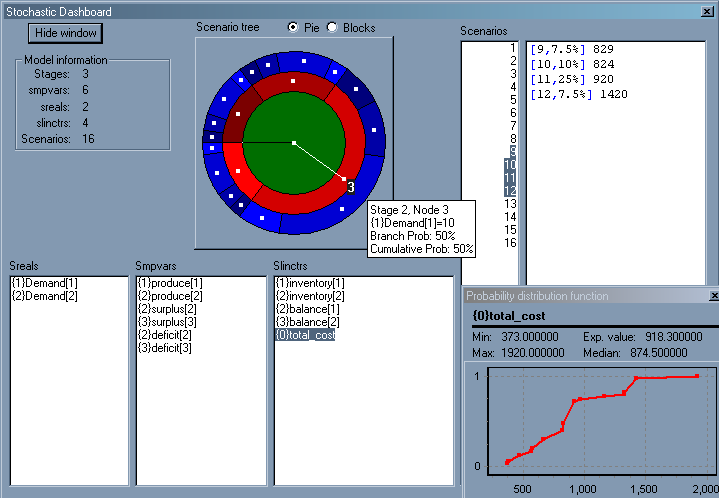
Figure 5.20: Stochastic dashboard

One may interactively aggregate and delete scenarios in IVE after scenario generation and before optimization. The user must check the option Pause to prune scenario tree manually in IVE in order to perform these scenario-pruning operations.

SP/m42026068.png

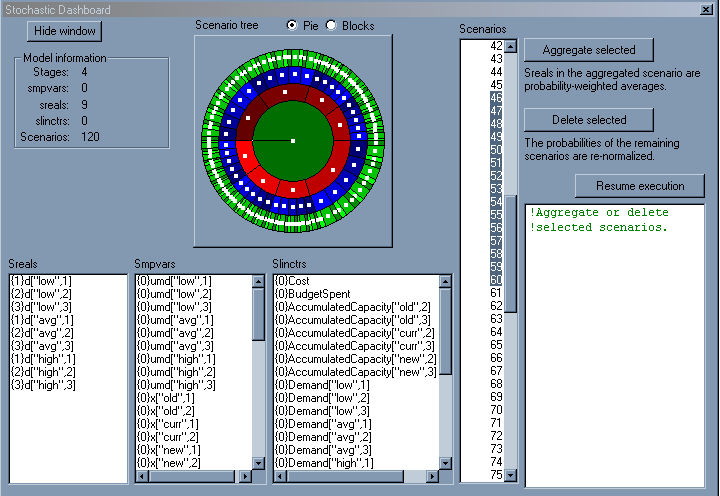
Figure 5.21: Aggregation and Deletion in IVE

Aggregation

Once the model is running in the pause mode, users may click on multiple numbers of nodes to select the scenarios to be aggregated. If the button Aggregate selected on the dashboard is pressed, then aggregation is performed automatically and the scenario tree is updated. As mentioned earlier, the new aggregated scenario probability is sum of all the probabilities of the scenarios that were aggregated, and the aggregated sprand are sum of the corresponding conditional–probability weighted sprand.

Deletion

In the pause mode, users may select scenarios to be deleted. One may use the `ctrl' key on the keyboard for multiple selections of scenarios from the scenario list or from the scenario tree, and then press the button Delete selected. The remaining scenario and conditional probabilities are re-normalized, and the scenario tree is updated automatically. Note that both of these operations can be performed interactively, and multiple times as long as a valid scenario tree exists. The equivalent mmsp functions are displayed in the text box on the dashboard, which users may copy in their model to replicate the same behavior in the next run. Users may resume execution of the model by pressing the button Resume execution on the dashboard.

Matrix View

Users may view the underlying expanded matrix in the Matrix tab in IVE. The matrix view provides List view to see the solution, and the Graphical original and Graphical presolved to visualize the original and the pre-solved matrix. The user must select the option for viewing these matrices in IVE. As mentioned in Section Expanding the underlying deterministic model, the matrix can be expanded according to nodes or scenario. In the former case, the variables and constraints are prefixed by their node numbers, whereas in the latter case they are prefixed by their scenario numbers. For the purpose of clarity, these numbers are enclosed in square brackets.

Other standard features

The following standard features of IVE can be used for writing and analyzing the stochastic models:


[Next] [Index]
If you have any comments or suggestions about these pages, please send mail to docs@dashoptimization.com.